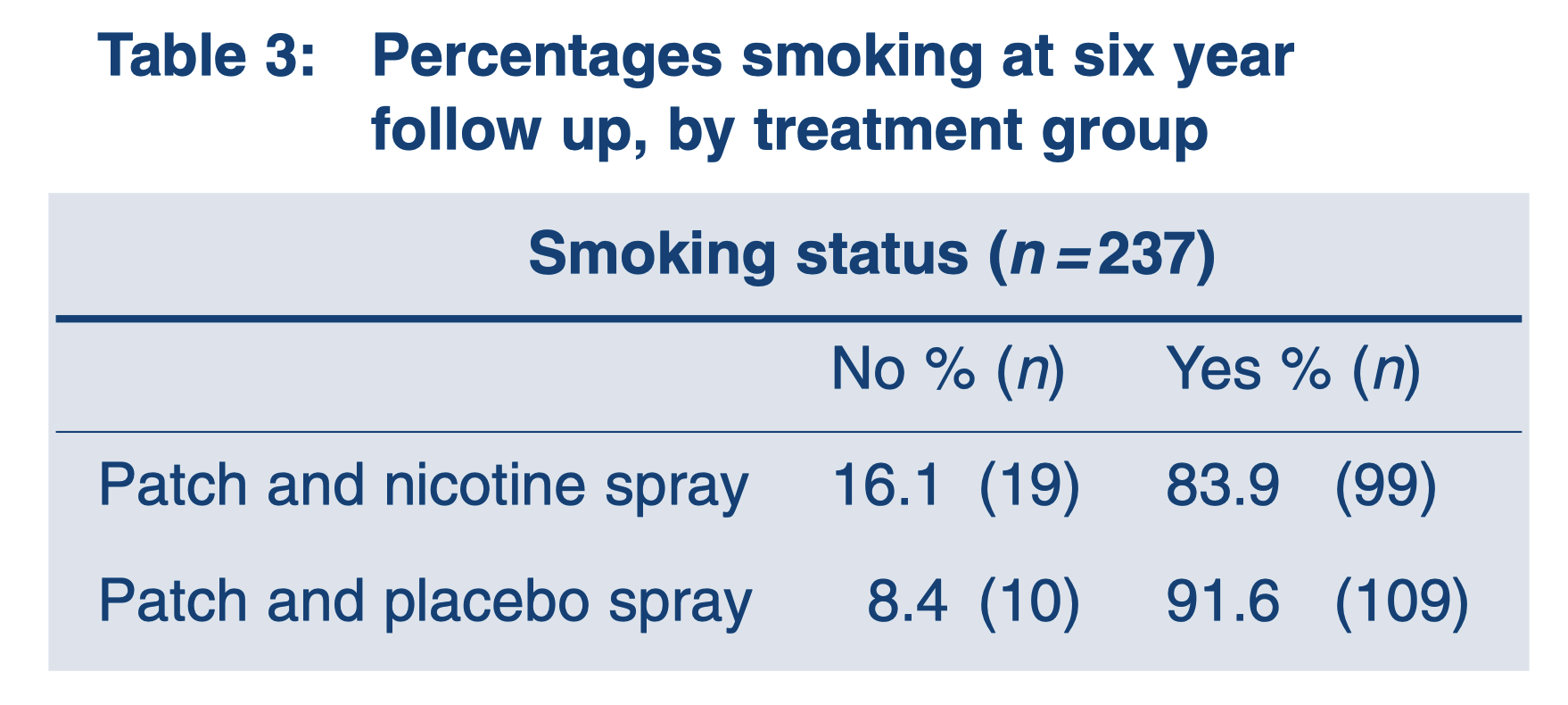39 확률(Probability), 오즈(Odds), 가능도(likelihood)
이 글은 Harrison’s Principles of Internal Medicine.(Loscalzo et al. 2022)과 (Cook and Sheikh 2000)의 글을 주로 참고해서 정리했다.
39.1 비(ratio)와 비율(proportion)의 차이
- 비(ratio)는 두 수의 크기를 비교한다. 예를 들어, 10:5는 2:1의 비이다.
\[ \text{ratio} = \frac{a}{b} \]
- 비율(proportion)은 전체에서 특정 부분의 크기를 나타낸다. 예를 들어, 10개의 항목 중 2개가 특정 조건을 만족하면, 그 비율은 2/10 = 0.2 또는 20%이다.
\[ \text{proportion} = \frac{\text{특정 부분의 크기}}{\text{전체 크기}} = \frac{2}{10} = 0.2 = 20\% \]
39.2 확률(probability)과 오즈(odds)의 차이
통계학에서 확률(probability)은 특정 사건이 발생할 가능성을 나타낸다. 주사위를 던져 6이 나올 확률은 1/6이다. 확률은 0에서 1 사이의 값을 가지며, 0은 사건이 절대 발생하지 않음을, 1은 사건이 반드시 발생함을 의미한다. \[ P(A) = \frac{\text{사건 A가 발생하는 경우의 수}}{\text{전체 경우의 수}} \]
의학에서는 어떤 개인이 병에 걸릴 확률을 Risk라고 한다. 예를 들어, 100명 중 10명이 병에 걸린다면, 그 병에 걸릴 Risk는 10%이다. 즉, Risk는 확률의 한 형태이다.
\[ \text{Risk} = \frac{\text{Numoer of cases}}{\text{Total population}} = \frac{10}{100} = 0.1 = 10\% \]
통계학에서 오즈(odds)는 특정 사건이 발생할 확률과 발생하지 않을 확률의 비이다. 식을 보면 오즈는 0에서 무한대 사이의 값을 가지며, 0은 사건이 절대 발생하지 않음을, 무한대는 사건이 반드시 발생함을 의미한다. \[ \text{odds} = \frac{P(A)}{1 - P(A)} \]
의학에서 사용할 때는 오즈(odds)도 같은 개념으로, 질병이 발생할 확률과 발생하지 않을 확률의 비로 정의된다. 예를 들어, 100명 중 10명이 병에 걸렸다면, 그 병에 걸릴 오즈는 10:90 또는 1:9이다.
\[ \frac{\frac{10}{100}}{\frac{90}{100}} = \frac{10}{90} = \frac{1}{9} \]
\[ \text{odds} = \frac{\text{Number of cases}}{\text{Number of non-cases}} = \frac{10}{90} = \frac{1}{9} \]
다음 표에서 Risk와 오즈(Odds)를 구해 보자.
Risk: \(\frac{34}{401} = 0.0848 = 8.48\%\)
Odds: \(\frac{34}{401 - 34} = \frac{34}{367} = 0.0926 = 9.26\%\)
39.3 비율의 비율: Relative Risk와 Odds Ratio
Relative Risk(Risk Ratio)와 Odds Ratio는 두 그룹 간의 비교를 위해 사용되는 통계적 지표이다.
- Relative Risk (RR)는 두 그룹 간의 Risk의 비이다.
- Odds Ratio (OR)는 두 그룹 간의 Odds의 비이다.
두 그룹이란 보통 노출 그룹과 비노출 그룹 또는 질병이 있는 그룹과 질병이 없는 그룹을 의미한다.
Relative Risk는 노출 그룹과 비노출 그룹의 Risk를 비교하는 지표이다. \[ \text{RR} = \frac{\text{Risk of exposed group}}{\text{Risk of non-exposed group}} = \frac{\frac{a}{a+b}}{\frac{c}{c+d}} \]
Odds Ratio는 노출 그룹과 비노출 그룹의 Odds를 비교하는 지표이다. \[ \text{OR} = \frac{\text{Odds of exposed group}}{\text{Odds of non-exposed group}} = \frac{\frac{a}{b}}{\frac{c}{d}} \]
Relative Risk와 Odds Ratio 모두 1보다 크면 노출 그룹에서 질병이 발생할 위험이 더 높다는 것을 의미하고, 1보다 작으면 노출 그룹에서 질병이 발생할 위험이 더 낮다는 것을 의미한다.
다음과 같은 표가 주어졌을 때 Relative Risk와 Odds Ratio를 계산해 보자.
- Relative Risk (RR): \(\frac{13/116}{21/285} = \frac{0.11}{0.07} = 1.52\)
- Odds Ratio (OR): \(\frac{13/103}{21/264} = \frac{0.126}{0.079} = 1.60\)
39.4 Number Needed to Treat (NNT)
치료는 환자의 질병 위험도를 낮출 것이고, 유해 인자는 환자의 질병 위험도를 높일 것이다. 어떤 치료의 효과가 얼마가 될지, 또는 어떤 유해 인자의 효과가 얼마나 클지를 보는 지표가 필요할 수 있다. Number Needed to Treat (NNT)는 치료 효과를 평가하는 데 사용되는 지표이다. 특정 치료를 통해 한 명의 환자를 치료하기 위해 필요한 평균 환자 수를 나타낸다. NNT가 낮을수록 치료 효과가 크다는 것을 의미한다.
NNT는 다음과 같이 계산된다: \[ \text{NNT} = \frac{1}{\text{Absolute Risk Reduction (ARR)}} \]
Absolute Risk Reduction (ARR)는 치료 그룹과 대조 그룹 간의 위험 차이를 나타낸다. 예를 들어, 치료 그룹에서 40%의 환자가 치료 효과를 보이고, 대조 그룹에서 30%의 환자가 치료 효과를 보였다면, ARR는 10%가 된다. 따라서 NNT는 다음과 같이 계산된다: \[ \text{ARR} = \text{Risk in control group} - \text{Risk in treatment group} = 0.30 - 0.40 = -0.10 \]
\[ \text{NNT} = \frac{1}{0.10} = 10 \]
NNT가 10이라는 것은, 이 치료를 통해 한 명의 환자를 치료하기 위해 평균적으로 10명의 환자를 치료해야 한다는 것을 의미한다. 즉, NNT가 낮을수록 치료 효과가 크다는 것을 나타낸다.
다음 표에서 NNT를 계산해 보자.
- 플라세보 그룹의 Risk: \(\frac{109}{10+109} = 0.9167\)
- 치료 그룹의 Risk: \(\frac{99}{19+99} = 0.8381\)
- Absolute Risk Reduction (ARR): \(0.9167 - 0.8381 = 0.0786\)
- NNT: \(\frac{1}{0.0786} \approx 12.7\) 즉, 이 치료를 통해 한 명의 환자를 치료하기 위해 평균적으로 약 13명의 환자를 치료해야 한다는 것을 의미한다.
39.5 가능도(likelihood)
가능도(likelihood)는 주어진 데이터가 특정 모델 또는 가설 하에서 얼마나 가능성이 있는지를 나타내는 지표이다. 주어진 데이터가 특정 확률 분포를 따를 때 그 분포의 매개변수를 추정하는 데 사용되다(말이 어렵다😬).
진단 검사에서는 가능도는 민감도(sensitivity)와 거의 동일한 개념으로 사용된다. 즉, 특정 질병이 있는 환자가 검사에서 양성 결과를 보일 확률을 나타낸다. 즉 “주어진 데이터가 특정 확률을 따를 때”와 “특정 질병이 있는”는 동일한 맥락으로 받아들일 수 있다. 주어진 데이터가 있다는 전제하에서 어떤 것을 고려하는 것으로 이것은 조건부 확률의 일종이다. 진단 검사와 관련된 내용은 37장에서도 다루고 있으니 헷갈리는 경우 링크를 참고하자.
가능도는 다음과 같이 계산된다:
\[ \text{Likelihood} = P(\text{Data} | \text{Model}) = P(\text{Data} | \text{Hypothesis}) \]
이런 가능도는 통계학에서 매우 중요한 역할을 한다.
베이즈 통계학: 베이즈 통계학에서는 가능도를 사용하여 사후 확률(posterior probability)을 계산한다. 이는 주어진 데이터가 있을 때 특정 가설이 얼마나 가능성이 있는지를 평가하는 데 유용하다.
최대 우도 추정(Maximum Likelihood Estimation, MLE): MLE는 주어진 데이터에 대해 가능한 매개변수를 찾는 방법이다. 즉, 주어진 데이터가 가장 잘 설명되는 매개변수를 찾는다.
39.5.1 베이즈 정리(Bayes’ theorem)
베이즈 정리는 사전 확률(prior probability)과 가능도(likelihood)를 결합하여 사후 확률(posterior probability)을 계산하는 데 사용된다. 이는 주어진 데이터가 있을 때 특정 가설이 얼마나 가능성이 있는지를 평가하는 데 유용하다.
베이즈 정리는 다음과 같이 표현된다: \[ P(H | D) = \frac{P(D | H) \cdot P(H)}{P(D)} \]
베이즈 정리는 다음과 같은 요소로 구성된다.
- \(P(H | D)\): 사후 확률(posterior probability)
- \(P(D | H)\): 가능도(likelihood), 민감도
- \(P(H)\): 가설 \(H\)의 사전 확률(prior probability)
- \(P(D)\): 데이터 \(D\)의 전체 확률(marginal likelihood)
베이즈 정리는 주어진 데이터가 있을 때 가설의 가능성을 업데이트하는 데 사용되며, 이는 진단 검사에서 질병의 존재 여부를 평가하는 데 중요한 역할을 한다.
만약 유병률이 0.01(1%)인 질병에 대해 민감도가 0.9(90%)이고 특이도가 0.95(95%)인 검사가 있다고 해 보자. 어떤 환자가 검사에서 양성 결과를 보였을 때, 그 환자가 실제로 질병에 걸렸을 확률을 계산할 수 있다.
사전 확률(prior probability): 유병률 = 0.01
가능도(likelihood): 민감도 = 0.9
특이도 = 0.95
전체 확률(marginal likelihood):
\[ P(D) = P(D | H) \cdot P(H) + P(D | \neg H) \cdot P(\neg H)\] \[ P(D) = 0.9 \cdot 0.01 + (1 - 0.95) \cdot (1 - 0.01) = 0.009 + 0.0495 = 0.0585 \]사후 확률(posterior probability): \[ P(H | D) = \frac{P(D | H) \cdot P(H)}{P(D)} = \frac{0.9 \cdot 0.01}{0.0585} \approx 0.154 \]
39.5.2 검사의 반복과 Posterior가 Prior로 업데이트
위 검사를 한 번 시행하고 양성 결과가 나왔다고 가정하자. 이 때 사후 확률은 약 15.4%이다. 만약 이 검사를 다시 시행하고, 또 양성 결과가 나왔다면, 사후 확률을 업데이트할 수 있다.
이 때, 이전의 사후 확률을 새로운 사전 확률로 사용하여 다음과 같이 계산한다.
- 새로운 사전 확률(prior probability): 이전 사후 확률 = 0.154
- 새로운 가능도(likelihood): 민감도 = 0.9
- 전체 확률(marginal likelihood):
\[ P(D) = P(D | H) \cdot P(H) + P(D | \neg H) \cdot P(\neg H) \]
\[ P(D) = 0.9 \cdot 0.154 + (1 - 0.95) \cdot (1 - 0.154) = 0.1386 + 0.0423 = 0.1809 \]
- 새로운 사후 확률(posterior probability): \[ P(H | D) = \frac{P(D | H) \cdot P(H)}{P(D)} = \frac{0.9 \cdot 0.154}{0.1809} \approx 0.767 \] 즉, 두 번의 양성 결과를 받은 후, 그 환자가 실제로 질병에 걸렸을 확률은 약 76.7%로 증가한다.
39.6 혼동 행렬로 업데이트 하는 방법
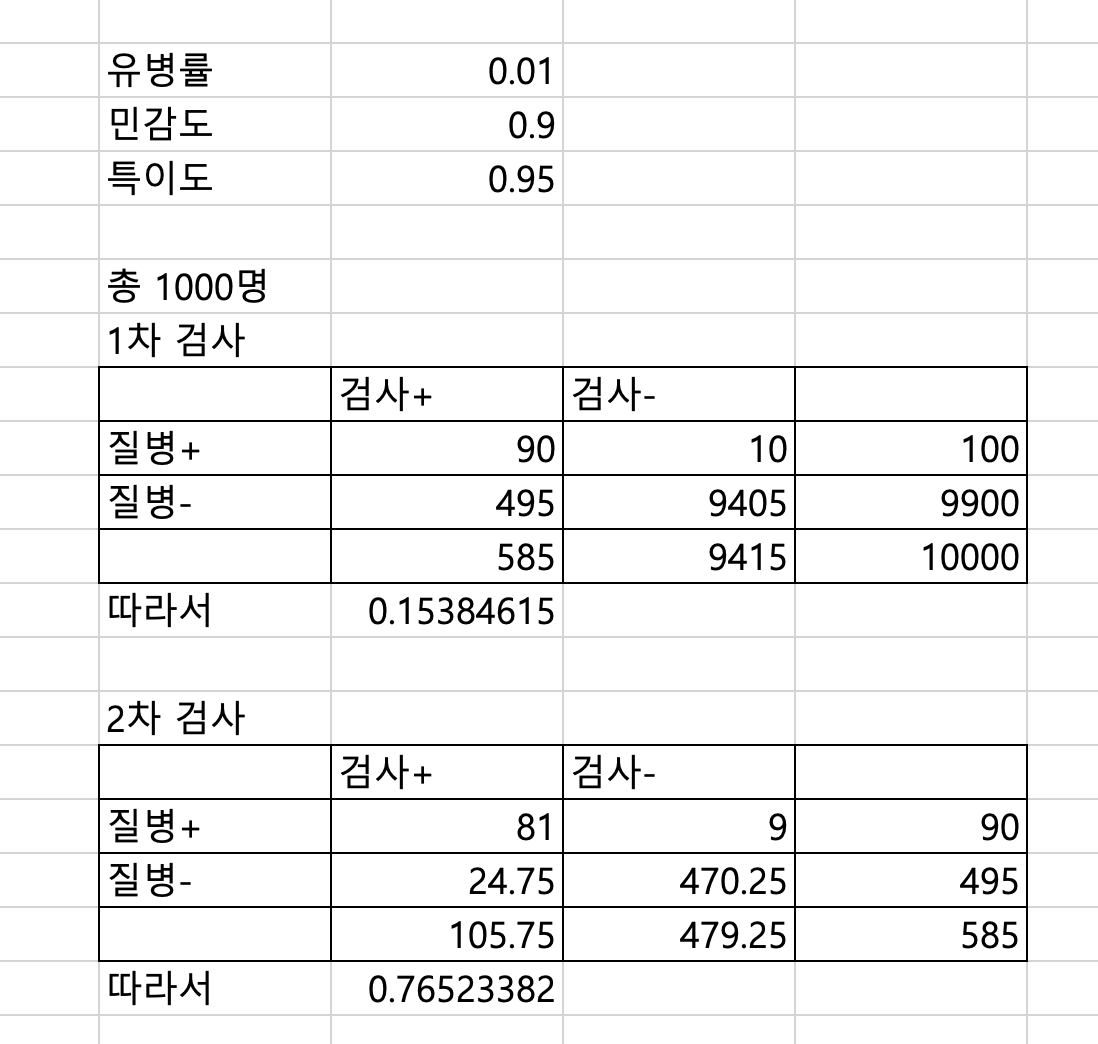
위와 똑같은 유병률이 0.01(1%)인 질병에 대해 민감도가 0.9(90%)이고 특이도가 0.95(95%)인 검사가 있다고 해 보자. 어떤 환자가 검사에서 양성 결과를 보였을 때, 그 환자가 실제로 질병에 걸렸을 확률을 혼동행렬로 계산해 보자.
39.6.1 오늘의 뇌는 어제의 뇌가 아니다!
베이즈 정리는 반복적인 검사를 통해 사후 확률을 업데이트하는 데 유용하다. 어쩌면 우리 뇌는 베이지안 머신일 수 있다. 매일매일 새로운 데이터를 통해 우리의 믿음과 확률이 업데이트되기에.