| A | B | response |
|---|---|---|
| A1 | B1 | a |
| A1 | B2 | b |
| A2 | B1 | c |
| A2 | B2 | d |
34 이원 분산분석(Two-way ANOVA)(작업중)
이원 분산분석(Two-Way ANOVA)은 두 개의 독립 변수와 하나의 종속 변수가 있을 때 사용된다. 이 분석은 각 독립 변수의 효과와 상호 작용 효과를 평가한다.
- 독립 변수: 두 개의 범주형 변수
- 종속 변수: 하나의 연속형 변수
뒤에서 보겠지만 R 언어로 이원 분산 분석을 하는 것은 아주 간단하다. 구체저인 방법은 잠시 미루고, 이런 이원 분산분석이 행해지는 상황과 결과 해석에 필요한 기초적인 개념을 먼저 설명하고자 한다.
34.1 요인 설계(Factorial Design)
요인 설계(Factorial Design)는 두 개 이상의 독립 변수를 동시에 고려하여 실험을 설계하는 방법이다. 각 독립 변수의 수준(level)을 조합하여 다양한 조건을 생성하고, 이 조건에서 종속 변수를 측정한다. 이 방법은 각 독립 변수의 주효과(main effect)와 상호 작용 효과(interaction effect)를 평가할 수 있다.
주효과(main effect)와 상호 작용 효과(interaction effect) (by ChatGPT)
-
Main Effect (주효과)
- 정의: 각 독립 변수가 종속 변수에 미치는 독립적인 영향을 의미합니다. 즉, 다른 독립 변수의 수준에 관계없이 특정 독립 변수의 수준 변화가 종속 변수에 미치는 평균적인 효과를 평가합니다.
- 예시: 만약 species와 sex가 독립 변수이고 body_mass_g가 종속 변수라면, species의 주효과는 성별에 관계없이 종의 차이가 체중에 미치는 영향을 나타냅니다. 마찬가지로, sex의 주효과는 종에 관계없이 성별 차이가 체중에 미치는 영향을 나타냅니다.
-
Interaction Effect (상호 작용 효과)
- 정의: 두 개 이상의 독립 변수가 결합하여 종속 변수에 미치는 영향을 의미합니다. 상호 작용 효과는 한 독립 변수의 효과가 다른 독립 변수의 수준에 따라 달라지는지를 평가합니다.
- 예시: species와 sex 간의 상호 작용 효과는 종에 따른 체중 차이가 성별에 따라 달라지는지를 나타냅니다. 즉, 어떤 종에서는 성별에 따른 체중 차이가 크지만, 다른 종에서는 그렇지 않을 수 있습니다.
예를 들어, 두 개의 독립 변수 A와 B가 있을 때, 각 변수의 수준이 다음과 같다고 가정해 보자.
- 독립 변수 A: A1, A2
- 독립 변수 B: B1, B2
이 경우, 가능한 조합은 다음과 같다.
또는 다음과 같이 크로스 테이블(cross table)로 나타낼 수도 있다.
독립 변수 A와 B의 각 수준 조합에 대해 피시험자를 무작위로 배정하고 종속 변수를 측정한다. A라는 요인의 효과를 연구를 하고, B라는 효과를 보는 연구를 하고, A와 B의 상호 작용 효과를 각각 따로 하는 것보다, 두 요인을 동시에 고려하기 때문에 표본의 수를 줄일 수 있고, 자원을 절약할 수 있는 방법으로 알려져 있다. 임상 연구, 동물 실험, 사회 과학 연구 등 다양한 분야에서 사용된다.
그런데, 이런 실험 설계를 하는 경우 각 요인의 수준이 서로 독립적이지 않을 수 있다. 예를 들어, A1과 B1의 조합에서 A1의 효과가 B1의 효과에 영향을 미칠 수 있다. 그래서 이런 연구에서는 상호 작용 효과(interaction effect)를 고려해야 한다.
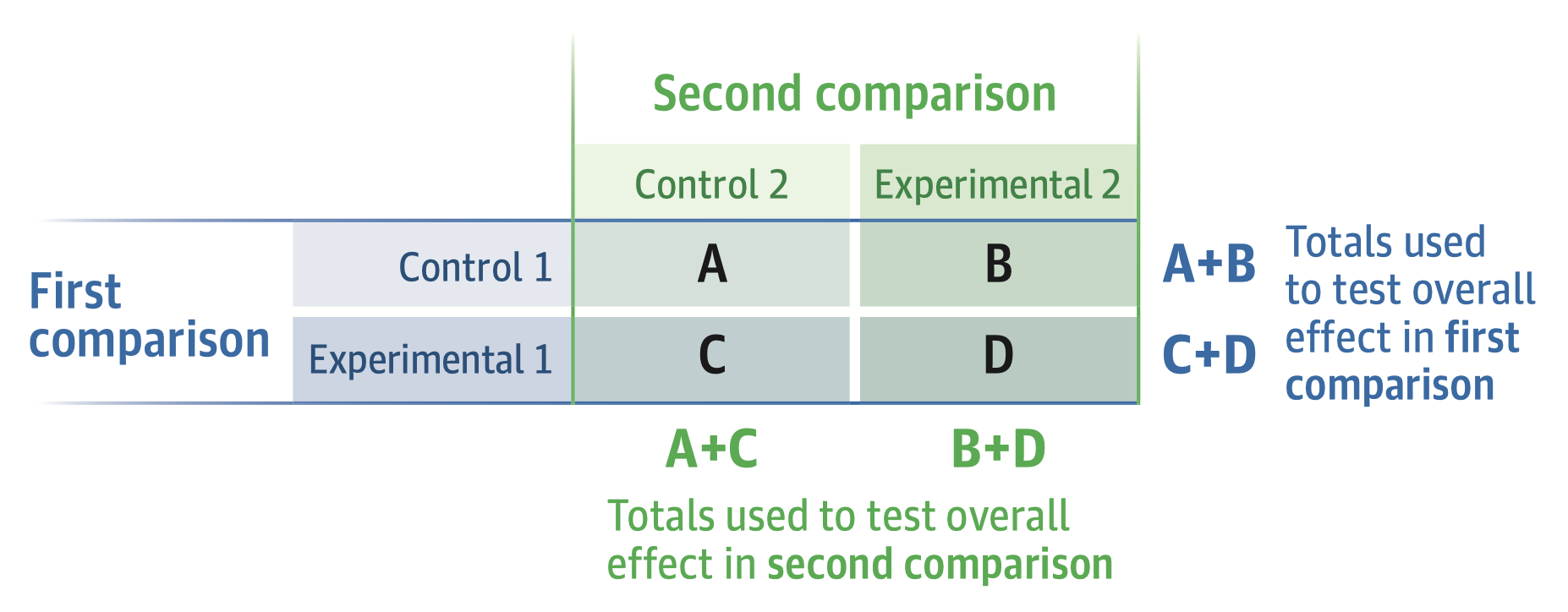
그림 34.1에서 보듯이, 가로 방향으로 더한 값 A+B, C+D는 첫 번재 요인의 주효과(main effect)를 비교하는 데 사용되고, 세로 방향으로 더해진 A+C, B+D는 두 번째 요인의 주효과를 비교하는 데 사용된다. 이때, 각 요인의 주효과는 독립적으로 평가된다. 그러나 두 요인의 조합에 따라 종속 변수의 값이 달라질 수 있는데 이것을 두 요인의 상호 작용 효과(interaction effect)라고 한다.
상호 작용 효과는 베이스 R의 interaction.plot() 함수를 사용하여 시각화할 수 있다. 이 함수는 두 개의 독립 변수의 수준에 따른 종속 변수의 평균 값을 그래프로 나타낸다. 그래프에서 선들이 평행하면 상호 작용 효과가 없다고 판단할 수 있다. 반면, 선들이 교차하거나 평행하지 않으면 상호 작용 효과가 있다고 판단한다.
예를 들어, 펭귄 데이터셋에서 species와 sex에 따른 body_mass_g의 평균 값을 비교하는 경우, 다음과 같이 할 수 있다.
library(tidyverse)
library(palmerpenguins)
data("penguins", package = "palmerpenguins")
penguins <- na.omit(penguins)
penguins |>
group_by(species, sex) |>
summarise(response = mean(body_mass_g, na.rm = TRUE))# A tibble: 6 × 3
# Groups: species [3]
species sex response
<fct> <fct> <dbl>
1 Adelie female 3369.
2 Adelie male 4043.
3 Chinstrap female 3527.
4 Chinstrap male 3939.
5 Gentoo female 4680.
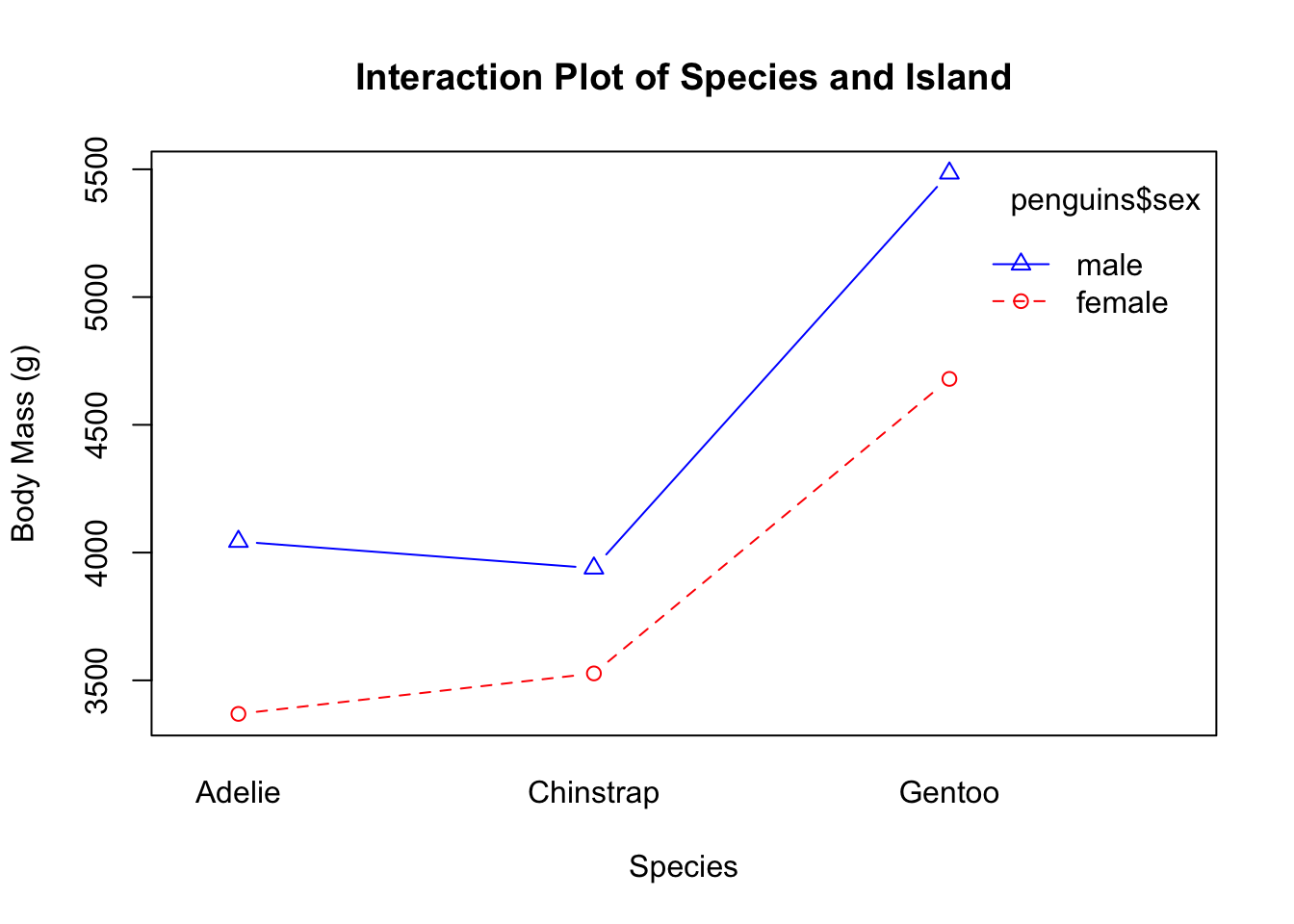
6 Gentoo male 5485.베이스 R의 interaction.plot() 함수를 사용하여 플롯팅하였다. 위에서 구한 평균 값을 사용하여 상호 작용 그래프를 그릴 수 있다.
interaction.plot(
x.factor = penguins$species,
trace.factor = penguins$sex,
response = penguins$body_mass_g,
type = "b",
pch = c(1, 2),
col = c("red", "blue"),
main = "Interaction Plot of Species and Island",
xlab = "Species",
ylab = "Body Mass (g)"
)
위 결과를 보면 선들이 평행하지 않아, species와 sex 간에 상호 작용 효과가 존재한다고 판단할 수 있다. 즉, 종에 따라 성별에 따른 체중 차이가 다르게 나타날 수 있다는 것이다.
34.2 이원 분산분석의 목적과 가설
이원 분산분석의 목적은 두 개의 독립 변수의 주효과와 상호 작용 효과를 평가하는 것을 목적으로 한다. 즉, 다음 효과를 동시에 검정한다. 종속 변수에 대한 독립 변수의 효과가 없다는 귀무가설, 서로 상호작용 효과가 없다는 귀무가설을 세운다.
-
주효과 가설 (Main Effect Hypothesis):
- 독립 변수 A의 주효과
- 독립 변수 B의 주효과
-
상호 작용 효과 가설 (Interaction Effect Hypothesis):
- 독립 변수 A와 B의 상호 작용 효과
34.3 이원 분산분석의 가정
이원 분산분석의 가정은 33장에서 설명한 것과 같다. 이 가정을 만족하는지 체크하는 것도 같은 방법을 사용한다.
- 정규성 (Normality): 종속 변수의 분포가 정규 분포를 따른다. 각 그룹의 종속 변수 값이 정규 분포를 따르는지 확인해야 한다.
- 등분산성 (Homogeneity of Variance): 각 그룹의 분산이 동일하다. 즉, 독립 변수의 수준에 관계없이 종속 변수의 분산이 동일해야 한다.
- 독립성 (Independence): 각 관측치는 서로 독립적이다. 즉, 한 관측치가 다른 관측치에 영향을 미치지 않아야 한다.
34.4 R 포뮬러로 상호 작용을 표현하기
27장에서 설명했지만, R 포뮬러(formula)에서는 상호 작용(interaction effect)은 : 또는 * 기호를 사용하여 표현한다.
-
A:B: A와 B의 상호 작용을 나타냄 -
A*B: A와 B의 주효과와 상호 작용을 모두 포함(A + B + A:B와 동일함)
그래서 펭귄 데이터셋에서 체중(body_mass_g)에 대하여 species와 sex라는 두 개의 독립 변수의 상호 작용을 분석하고자 한다면, 다음과 같이 포뮬러를 작성한다.
body_mass_g ~ species * sex또는 다음과 같이 쓸 수도 있다.
body_mass_g ~ species + sex + species:sex이런 R 포뮬러에 따른 이원 분산분석은 다음 귀무가설을 가지고 검정을 수행한다.
-
주효과 가설:
-
species의 주효과가 없다:sex를 고려하지 않았을 때species가body_mass_g에 미치는 영향이 없다. -
sex의 주효과가 없다:species를 고려하지 않았을 때sex가body_mass_g에 미치는 영향이 없다.
-
-
상호 작용 효과 가설:
-
species와sex의 상호 작용 효과가 없다.-
species가body_mass_g에 미치는 영향이sex에 따라 달라지지 않는다. -
sex가body_mass_g에 미치는 영향이species에 따라 달라지지 않는다.
-
-
34.5 이원 분산분석(Two-way ANOVA) 수행하기
이원 분산분석을 수행하기 위해서는 aov() 함수를 사용한다. 이 함수는 ANOVA 모델을 적합시키고, 결과를 반환한다.
Df Sum Sq Mean Sq F value Pr(>F)
species 2 145190219 72595110 758.358 < 2e-16 ***
sex 1 37090262 37090262 387.460 < 2e-16 ***
species:sex 2 1676557 838278 8.757 0.000197 ***
Residuals 327 31302628 95727
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Two-way ANOVA 결과 해석
이원 분산분석(Two-way ANOVA)의 결과를 해석하는 방법은 다음과 같다.(by ChatGPT)
A two-way analysis of variance (ANOVA) was conducted to examine the effects of species and sex on penguin body mass (body_mass_g). There was a significant main effect of species on body mass, F(2, 327) = 261.02, p < .001. The main effect of sex was also significant, F(1, 327) = 208.65, p < .001. Additionally, the interaction between species and sex was statistically significant, F(2, 327) = 12.37, p < .001. These results indicate that both species and sex have significant effects on penguin body mass, and that the effect of sex varies by species.
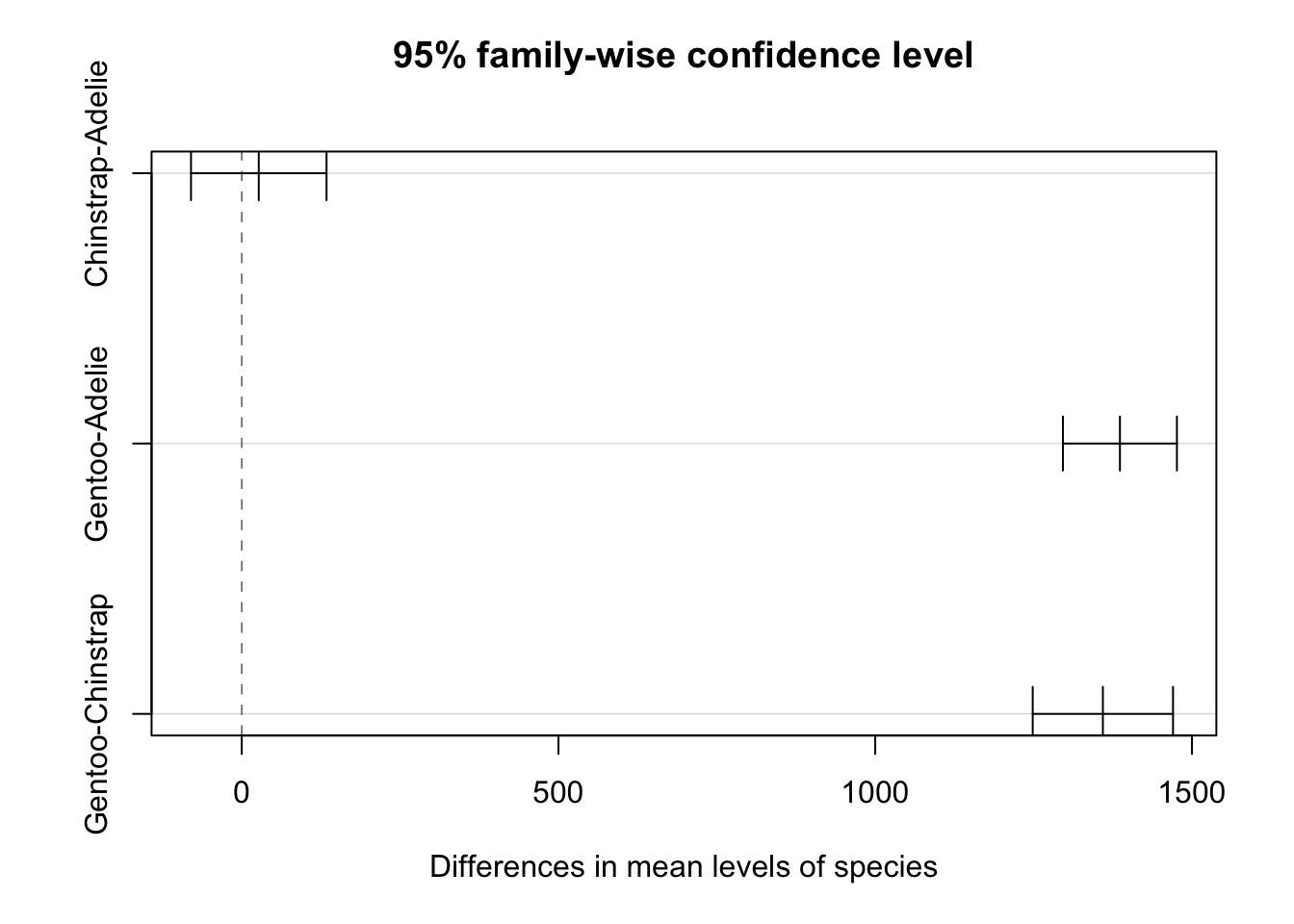
Tukey의 HSD(Honestly Significant Difference) 검정을 사용하여 사후 분석(post-hoc analysis)을 수행할 수 있다. 이 검정은 그룹 간의 차이를 비교하는 데 사용된다.
TukeyHSD(result, which="species") Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = body_mass_g ~ species * sex, data = penguins)
$species
diff lwr upr p adj
Chinstrap-Adelie 26.92385 -80.0258 133.8735 0.8241288
Gentoo-Adelie 1386.27259 1296.3070 1476.2382 0.0000000
Gentoo-Chinstrap 1359.34874 1248.6108 1470.0866 0.0000000
TukeyHSD(result, which="sex") Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = body_mass_g ~ species * sex, data = penguins)
$sex
diff lwr upr p adj
male-female 667.4577 600.7462 734.1692 0df <- na.omit(penguins)
result <- aov(body_mass_g ~ sex * species, data = df)
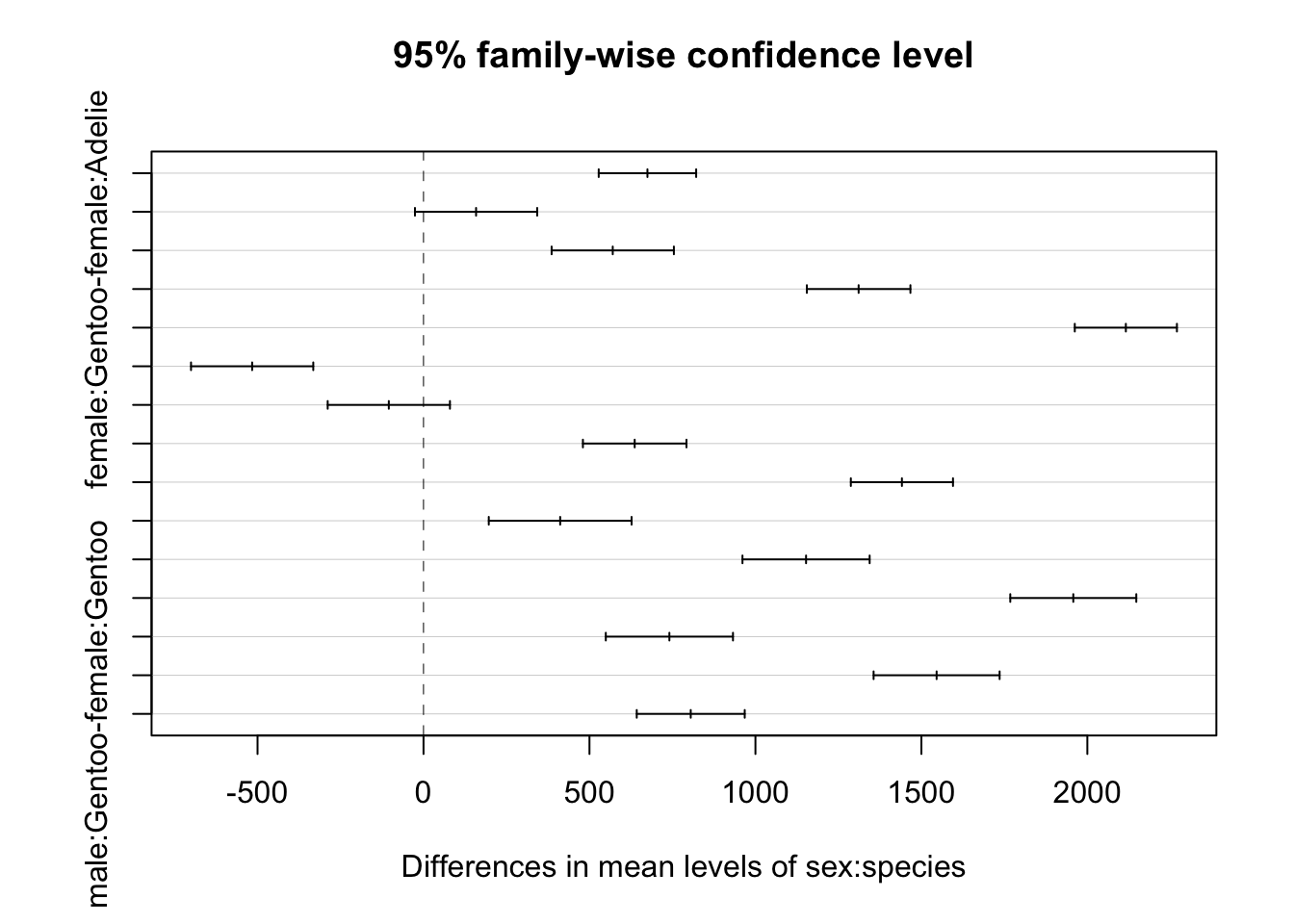
TukeyHSD(result, which = "sex:species") Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = body_mass_g ~ sex * species, data = df)
$`sex:species`
diff lwr upr p adj
male:Adelie-female:Adelie 674.6575 527.8486 821.4664 0.0000000
female:Chinstrap-female:Adelie 158.3703 -25.7874 342.5279 0.1376213
male:Chinstrap-female:Adelie 570.1350 385.9773 754.2926 0.0000000
female:Gentoo-female:Adelie 1310.9058 1154.8934 1466.9181 0.0000000
male:Gentoo-female:Adelie 2116.0004 1962.1408 2269.8601 0.0000000
female:Chinstrap-male:Adelie -516.2873 -700.4449 -332.1296 0.0000000
male:Chinstrap-male:Adelie -104.5226 -288.6802 79.6351 0.5812048
female:Gentoo-male:Adelie 636.2482 480.2359 792.2606 0.0000000
male:Gentoo-male:Adelie 1441.3429 1287.4832 1595.2026 0.0000000
male:Chinstrap-female:Chinstrap 411.7647 196.6479 626.8815 0.0000012
female:Gentoo-female:Chinstrap 1152.5355 960.9603 1344.1107 0.0000000
male:Gentoo-female:Chinstrap 1957.6302 1767.8040 2147.4564 0.0000000
female:Gentoo-male:Chinstrap 740.7708 549.1956 932.3460 0.0000000
male:Gentoo-male:Chinstrap 1545.8655 1356.0392 1735.6917 0.0000000
male:Gentoo-female:Gentoo 805.0947 642.4300 967.7594 0.0000000
Tukey의 HSD(Honestly Significant Difference) 검정 결과 해석 (by ChatGPT)