32  분산 분석의 기초: 제곱합(sum of squares), 자유도(df), 다중비교(multiple comparison)

이 장에서는 분산 분석(ANOVA)에서 제곱합(sum of squares)과 자유도(degree of freedom)의 개념에 대해 설명한다. 둘 모두 분산 분석에서 매우 중요한 개념이다. 다음은 어느 실험 계획 책에서 인용한 예이다(Lazic 2016).

library(tidyverse)
library(showtext)
font_add_google("Nanum Gothic", "nanumgothic")
showtext_auto()

간단한 데이터셋을 만들어 보자. x라는 팩터 변수가 있고, y라는 결과 변수(종속 변수)가 있다.

y <- c(6, 2, 3, 1, 4, 8, 7, 9)
x <- factor(rep(c("A", "B"), each = 4))
df <- tibble(y, x)
df

# A tibble: 8 × 2
      y x    
  <dbl> <fct>
1     6 A    
2     2 A    
3     3 A    
4     1 A    
5     4 B    
6     8 B    
7     7 B    
8     9 B    

32.1 전체 제곱합(total sum of squares)

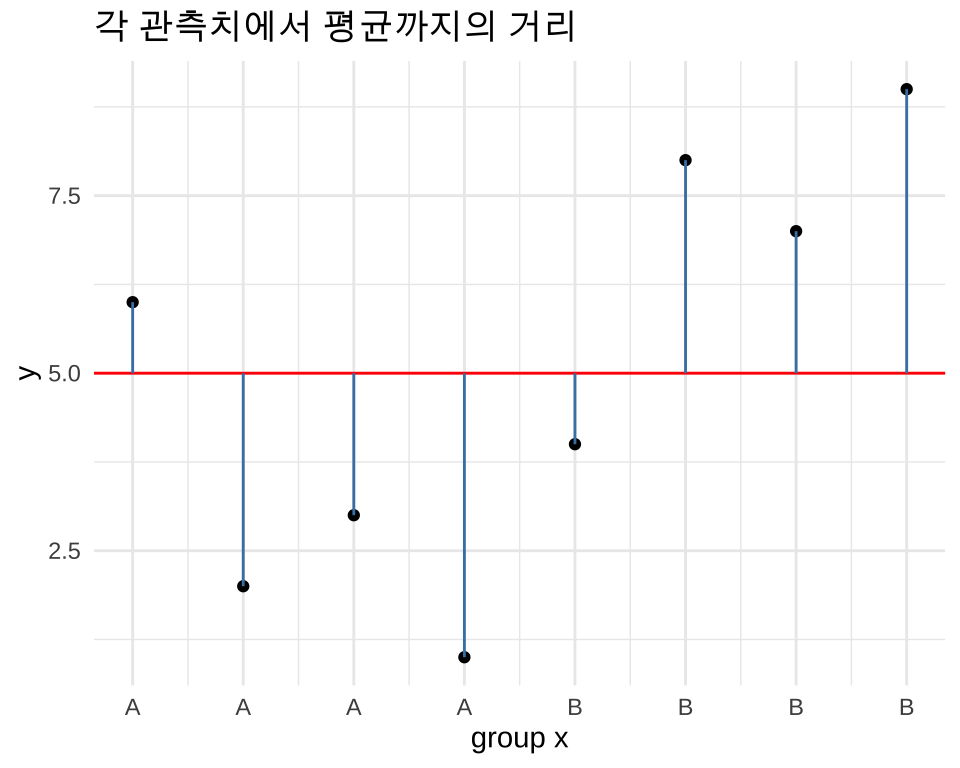
값들의 변동(variation)을 보기 위해서, 모든 관측치에 대해 전체 평균까지의 거리를 계산한 그래프를 그려보자.

df <- df %>%
    mutate(id = row_number())
df

# A tibble: 8 × 3
      y x        id
  <dbl> <fct> <int>
1     6 A         1
2     2 A         2
3     3 A         3
4     1 A         4
5     4 B         5
6     8 B         6
7     7 B         7
8     9 B         8

ggplot(df, aes(id, y)) +
    geom_point() +
    geom_hline(yintercept = mean(y), color = "red") +
    geom_segment(aes(x = id, xend = id, y = y, yend = mean(y)), color = "steelblue") +
    scale_x_continuous(breaks = 1:8, labels = x) +
    labs(
        x = "group x",
        title = "각 관측치에서 평균까지의 거리"
    ) +
    theme_minimal()

그림 32.1: 각 관측치에서 평균(빨간 선)까지의 거리(파란 선)

그래프에서 평균까지의 거리는 파란색 선으로 표시했다. 수식으로 표현하면 다음과 같다. \[ y_i - \bar{y} \]

이 값을 통계에서는 편차(deviation)라고 부른다. 편차는 관측치와 평균의 차이를 의미한다. 이런 편차의 합은 항상 0이 된다.

sum(df$y - mean(df$y))

[1] 0

통계학에서는 이 값을 사용하기 위해서 제곱을 취한다. 대표적인 경우가 분산(variance)이다. 분산은 편차의 제곱을 평균한 값이다. 수식으로 보면 다음과 같다.

분산은 다음과 같이 계산한다.

\[ \frac{1}{n-1} \sum_{i=1}^n (y_i - \bar{y})^2 \]

dev_y_squared <- (df$y - mean(df$y))^2
dev_y_squared

[1]  1  9  4 16  1  9  4 16

sum(dev_y_squared) / (length(df$y) - 1)

[1] 8.571429

var() 함수를 사용하면 분산을 바로 계산할 수 있다.

var(df$y)

[1] 8.571429

여기서 우리는 제곱합(sum of squares)을 알아 보려고 한다. 제곱합은 편차의 제곱을 모두 더한 값이다. 수식으로 표현하면 다음과 같은데 분산과 다른 점은 뭔가로 나누지 않았다는 점이다. 위 그래프에서 파란색 선의 길이를 제곱하여 더하면 제곱합이 된다.

\[ \sum_{i=1}^n (y_i - \bar{y})^2 \]

sum(dev_y_squared)

[1] 60

32.2 그룹별 평균을 고려한 제곱합(Residual Sum of Squares)

위 그래프는 x 요인을 고려하지 않고, 전체 그룹에서의 데이터의 변동을 보여주고 있다. 이제 그룹별로 데이터의 변동을 보기 위해서 그룹별로 평균을 계산하고, 평균까지의 거리를 계산해 보자.

ddf <- df %>%
    group_by(x) %>%
    mutate(mean_y = mean(y))
ddf

# A tibble: 8 × 4
# Groups:   x [2]
      y x        id mean_y
  <dbl> <fct> <int>  <dbl>
1     6 A         1      3
2     2 A         2      3
3     3 A         3      3
4     1 A         4      3
5     4 B         5      7
6     8 B         6      7
7     7 B         7      7
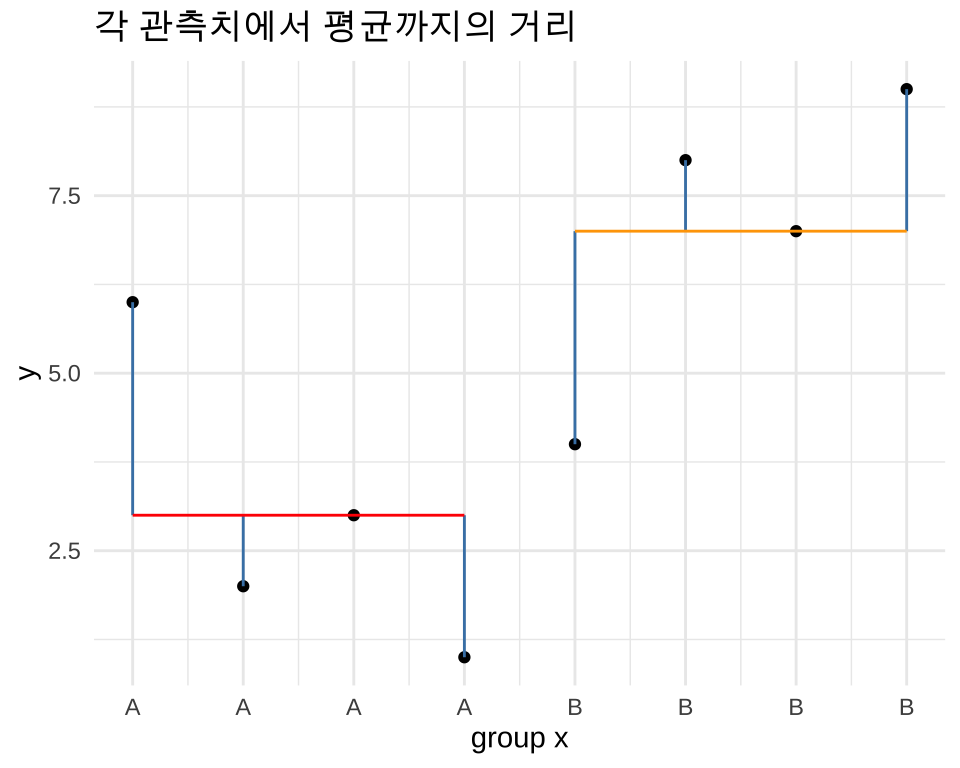
8     9 B         8      7

그룹의 평균에 대해서 각 관측치까지의 거리를 그려보자.

ggplot(ddf, aes(id, y)) +
    geom_point() +
    geom_segment(aes(x = id, xend = id, y = y, yend = mean_y), color = "steelblue") +
    annotate("segment", x = 1, xend = 4, y = 3, yend = 3, color = "red") +
    annotate("segment", x = 5, xend = 8, y = 7, yend = 7, color = "orange") +
    scale_x_continuous(breaks = 1:8, labels = x) +
    labs(x = "group x", title = "각 관측치에서 평균까지의 거리") +
    theme_minimal()

그림 32.2: 각 관측치에서 그룹별 평균까지의 거리(파란 선)

그룰별 평균까지의 거리를 제곱한 다음, 그 값들을 모두 더하면 잔차 제곱합(residual sum of squares)이 된다. 이 의미는 그룹별 평균을 고려한 후에도 남아있는 데이터의 변동을 의미한다.

부연하면, 상상해 보자. 그룹 A의 y값이 모두 3이고 그룹 B의 y값이 모두 7이라고 하자. 그러면 그룹별 평균을 고려한 후에는 남아있는 데이터의 변동은 없을 것이다(모두 빨간 평균 선에 놓일 것이다). 즉, 잔차 제곱합은 0이 된다.

ddf %>%
    group_by(x) %>%
    summarise(
        sum_y_squared = sum((y - mean_y)^2)
    )

# A tibble: 2 × 2
  x     sum_y_squared
  <fct>         <dbl>
1 A                14
2 B                14

32.3 그룹별 제곱합(sum of squares for each group)

전체 제곱합은 60이었고, 그룹을 고려한 잔차 제곱합은 28이었다. 그 차이 32를 그룹별 제곱합(sum of squares for each group)이라고 한다. 그룹별 제곱합은 그룹별 평균과 전체 평균의 차이를 제곱하여 그룹의 크기만큼 곱합 값을 합친 것이다.

\[ SSg = \sum_{i=1}^k n_i (\bar{y}_i - \bar{y})^2 \]

여기서 \(n_i\)는 i번째 그룹의 관측치의 개수이고, \(\bar{y}_i\)는 i번째 그룹의 평균이다. 즉, 그룹별 제곱합은 각 그룹의 평균이 전체 평균에서 얼마나 떨어져 있는지를 나타낸다.

그룹별 제곱합은 다음과 같이 계산할 수 있다.

ddf

# A tibble: 8 × 4
# Groups:   x [2]
      y x        id mean_y
  <dbl> <fct> <int>  <dbl>
1     6 A         1      3
2     2 A         2      3
3     3 A         3      3
4     1 A         4      3
5     4 B         5      7
6     8 B         6      7
7     7 B         7      7
8     9 B         8      7

4*(3-mean(ddf$y))^2 + 4*(7-mean(ddf$y))^2

[1] 32

그래서 일반적으로 다음과 같은 관계를 가진다.

\[ \text{Total Sum of Squares} = \text{Residual Sum of Squares} + \text{Sum of Squares for each group} \]

다음과 같이 표현할 수 있다. 즉, 그룹별 제곱합은 예측 변수의 효과를 반영한다. 잔차 제곱합은 예측 변수의 효과를 반영하지 못한 부분을 의미한다.

\[ \text{Total} = \text{Predictor(s)} + \text{Residual} \]

32.4 전체 데이터 변동에 기여하는 정도

다음과 같은 공식을 염두에 두면서 전체 데이터 변동성에 각 요소가 얼마 만큼 기여하는지 생각해 보자. \[ \text{Total} = \text{Predictor(s)} + \text{Residual} \]

그림 32.3은 생각하기 편하게 만든 간단한 그림이다.

그림 32.3: 전체 변동에 기여하는 정도를 생각하자!

실험1에서는 잔차보다 그룹별 제곱합이 더 큰 기여를 하고 있다. 실험2에서는 잔차보다 그룹별 제곱합이 더 작은 기여를 하고 있다. 이 기여도를 비율로 표현하고 싶다.

그런데 우리가 어떤 것을 서로 비교하고 싶다면 그것들의 단위를 맞출 필요가 있다. 이 경우에는 각 제곱합에서 자유도(degrees of freedom)를 나누어 주어야 한다. 그 나눈 값을 평균 제곱합(mean sum of squares)이라고 한다.

\[ \text{Mean Sum of Squares} = \frac{\text{Sum of Squares}}{\text{Degrees of Freedom}} \]

그래서 그룹별 평균 제곱합과 잔차 평균 제곱합의 비율을 가지고 데이터 변동성에 대한 기여도를 평가한다. 그것이 F-통계량(F-statistic)이다.

\[ F = \frac{SSg/df1}{SSr/df2}=\frac{MS_{\text{between}}}{MS_{\text{within}}} \]

F-통계량은 그룹별 평균 제곱합과 잔차 평균 제곱합의 비율을 가지고 데이터 변동성에 대한 기여도를 평가한다. 그리고 F-통계량은 항상 두 개의 자유도를 가지고 계산하게 된다.

32.5 자유도(degrees of freedom)

통계학에서 자유도(degrees of freedom)라는 개념을 자주 접하게 되는데, 직관적으로 이해하기는 쉽지 않다. 자유도는 통계적 추정에서 독립적으로 변할 수 있는 값의 개수를 의미한다.

예를 들어 3명의 체중을 측정하여 평균은 계산한다고 가정해 보자. 이때 3명의 체중을 x1, x2, x3라고 하면, 평균은 다음과 같이 계산된다. \[ \bar{x} = \frac{x_1 + x_2 + x_3}{3} \]

이 체중의 평균이 60이라고 가정해 보자. 그러면 x1, x2, x3 중에서 두 개의 값이 정해지면 나머지 하나는 자동으로 결정된다. 예를 들어 x1 = 55와 x2 = 65라고 하면, x3는 자동으로 60이 된다. 즉, 평균이 정해짐으로써 자유롭게 변할 수 있는 변수의 개수는 2개이다. 그래서 이 경우의 자유도는 2가 된다.

일반적으로 n개의 관측치가 있을 때, c개의 파라미터를 추정한다(즉, 조건이 c개이면), 자유도는 n - c가 된다. 일반적으로 다음과 같이 계산한다.

• 총 자유도는 전체 관측치의 개수에서 1을 뺀 값이다.
• 명목형 예측 변수에서 레벨(level)의 개수가 t개이면, 자유도는 t - 1이 된다.
• 연속형 예측 변수의 자유도는 1이다.
• 상호작용(interaction) 효과가 있는 경우, 자유도는 각 예측 변수의 자유도를 곱한 값이다. 예를 들어, x1과 x2가 각각 t1과 t2개의 레벨을 가지면, 상호작용의 자유도는 (t1 - 1) * (t2 - 1)이 된다.
• 잔차의 자유도는 총 자유도에서 예측 변수의 자유도를 뺀 값이다.

우리의 예제 df에서 자유도를 계산해 보자.

• 총 자유도 = 관측치의 개수 - 1 = 8 - 1 = 7
• 명목형 예측 변수 x의 자유도 = 레벨의 개수 - 1 = 2 - 1 = 1
• 잔차의 자유도 = 총 자유도 - 예측 변수의 자유도 = 7 - 1 = 6

32.6 R 함수: aov()

베이스 R에 있는 aov() 함수를 사용하면 분산 분석을 할 수 있다. 다음과 같이 사용하면 된다.

summary(aov(y ~ x, data = ddf))

            Df Sum Sq Mean Sq F value Pr(>F)  
x            1     32   32.00   6.857 0.0397 *
Residuals    6     28    4.67                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Df 열에서 자유도를 확인할 수 있다. Sum Sq 열에서 제곱합이다. Mean Sq 열에서 평균 제곱합인데, 제곱합을 자유도로 나눈 값이다. F value 열에서 F-통계량을 확인할 수 있다.

자유도 df1 =1, df2 = 6인 F-분포를 사용하여 p-값을 계산할 수 있다. F-분포는 두 개의 자유도를 가지며, 하나는 그룹의 개수에서 1을 뺀 값이고, 다른 하나는 잔차의 자유도이다. F-분포는 pf() 함수를 사용하여 p-값을 계산할 수 있다.

pf(6.86, df1 = 1, df = 6, lower.tail = FALSE)

[1] 0.0396308

32.7 다중비교(multiple comparison)

분산 분석에서 그룹 간의 차이를 확인한 후, 어떤 그룹이 다른 그룹과 차이가 있는지 확인하기 위해 다중비교(multiple comparison)를 수행한다. 이 부분은 뒤에서 설명한다. 먼저 다중 비교의 논리를 이해해 보자.

이 예제도 (Lazic 2016)에서 인용했다. 7개의 그룹이 있고, 각 그룹에 5개의 관측치가 있다.

set.seed(123)
response <- rnorm(7 * 5, 2)
group <- factor(rep(1:7, each = 5))
df2 <- tibble(response, group)
df2

# A tibble: 35 × 2
   response group
      <dbl> <fct>
 1    1.44  1    
 2    1.77  1    
 3    3.56  1    
 4    2.07  1    
 5    2.13  1    
 6    3.72  2    
 7    2.46  2    
 8    0.735 2    
 9    1.31  2    
10    1.55  2    
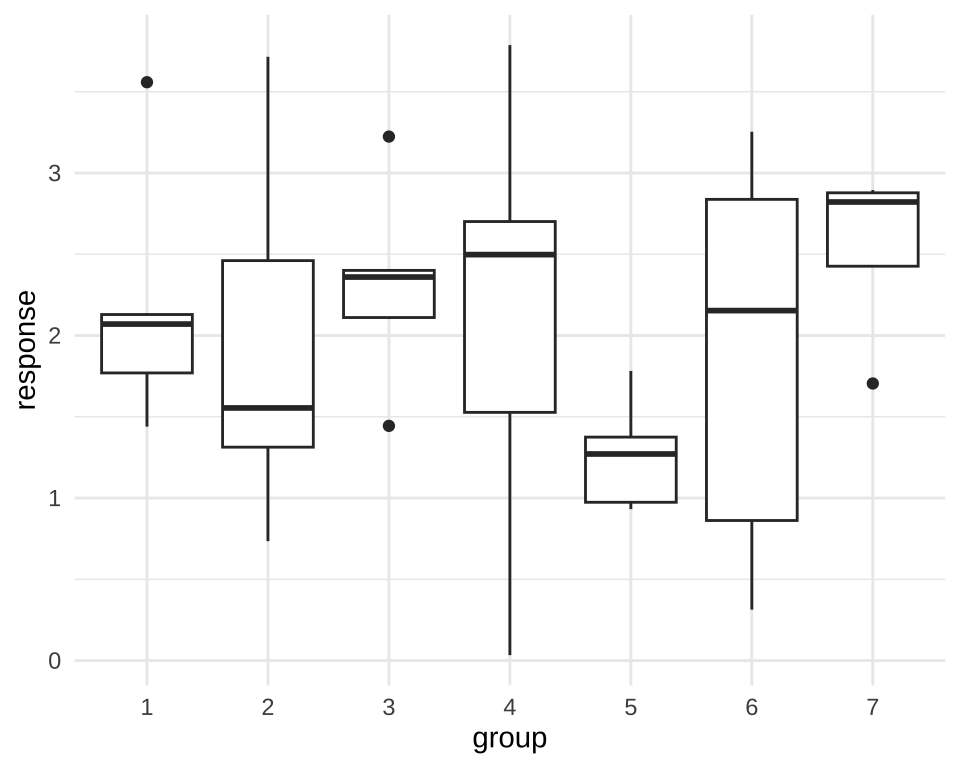
# ℹ 25 more rows

이것을 박스 플롯으로 그려보자.

ggplot(df2, aes(group, response)) +
    geom_boxplot() +
    labs(x = "group", y = "response") +
    theme_minimal()

분산 분석을 수행해 보자.

summary(aov(response ~ group, data = df2))

            Df Sum Sq Mean Sq F value Pr(>F)
group        6  4.923  0.8205     0.9  0.509
Residuals   28 25.521  0.9115               

결과는 약간 실망스럽다. 그룹간의 차이가 통계적으로 유의하지 않았다. 그런데… 위 그래프에서 5번째 그룹과 7번째 그룹의 차이가 가장 커 보인다. 뭔가 있을 것 같다.

이 두 그룹간의 차이가 통계적으로 유의미한지 확인하기 위해서 t.text() 함수를 사용하여 t-검정을 수행해 보자.

df3 <- df2 %>%
    filter(group %in% c(5, 7))
g1 <- df3 |>
    filter(group == 5) |>
    pull(response)
g2 <- df3 |>
    filter(group == 7) |>
    pull(response)
t.test(g1, g2, var.equal = TRUE)

    Two Sample t-test

data:  g1 and g2
t = -4.6607, df = 8, p-value = 0.001622
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.9109104 -0.6458763
sample estimates:
mean of x mean of y 
 1.266853  2.545247 

뭔가 통계적으로 유의미한 결과를 얻었다. 그런데… 이게 정말로 유의미한 결과일까?

32.7.1 임계값(critical value, \(\alpha\))

많은 경우 통계적 유의성을 판단하기 위해서 임계값(critical value, \(\alpha\))을 사용한다. 일반적으로 \(\alpha = 0.05\)를 사용한다. 즉, p-값이 \(0.05\)보다 작으면 통계적으로 유의미하다고 판단한다.

임계값을 이 \(\alpha\) 값과 비교하는 이유를 보자. 이 값은 귀무가설이 참인데도 불구하고 이를 기각할 확률을 확률인 1종 오류를 의미한다. 이 값을 0.05로 설정하면 귀무가설이 참인데도 불구하고 이를 기각할 확률이 5%까지 나오는 것은 허용하겠다는 것을 의미한다.

그런데 이 0.05라는 임계값을 그대로 사용하여 사용하여 조합에 의해서 만들어지는 여러 가지 비교 검정을 수행하면 문제가 발생한다. 예를 들어, 7개의 그룹이 있다고 가정해 보자. 이 경우 두 그룹을 비교하는 경우의 수는 다음과 같이 계산할 수 있다.

\[ \binom{7}{2} = \frac{7!}{2!(7-2)!} = 21 \]

통계 계산에서 어떤 사건이 적어도 한번(at least) 발생할 확률은 1에서 그 사건이 발생하지 않을 확률을 뺀 값이다. 즉, 21개의 비교 검정을 수행했을 때, 적어도 하나의 검정에서 1종 오류가 발생할 확률은 다음과 같이 계산할 수 있다. \[ 1 - (1 - 0.05)^{21} \approx 0.99 \] 즉, 21개의 비교 검정을 수행했을 때, 적어도 하나의 검정에서 1종 오류가 발생할 확률은 약 99%이다. 즉, 21개의 비교 검정을 수행했을 때, 적어도 하나의 검정에서 통계적으로 유의미한 결과가 나올 확률이 99%라는 것이다. 따라서, 이런 방법으로 통계 검정을 하면 1종 오류가 발생할 확률이 매우 높아지기 때문에 안 된다.

이런 문제를 해결하기 위해서 여러 가지 방법이 있다. 다중 비교는 이런 오류를 범하지 않기 위해 사용하는 방법으로, 1종 오류를 적절한 값 이내로 통제하여 그룹간의 차이를 검정한다.

32.7.2 다중 비교 방법

다중 비교 방법은 여러 가지가 있다. 그 가운데 Tukey’s HSD (Honest Significant Difference)은 그룹 간의 평균 차이를 비교하는 방법으로, 그룹 간의 차이가 통계적으로 유의미한지 확인한다. 이 방법은 그룹 간의 평균 차이를 비교할 때 가장 많이 사용된다.

penguins <- palmerpenguins::penguins
glimpse(penguins)

Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
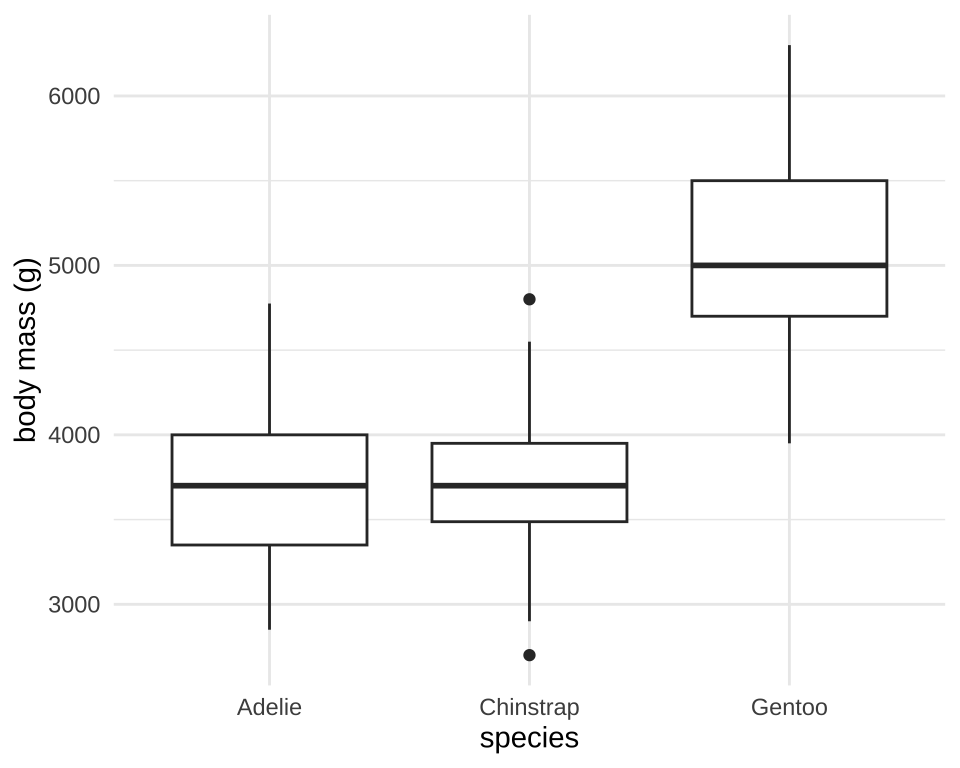
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

species에 따른 body_mass_g의 차이를 box plot으로 그려보자.

ggplot(penguins, aes(species, body_mass_g)) +
    geom_boxplot() +
    labs(x = "species", y = "body mass (g)") +
    theme_minimal()

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_boxplot()`).

분산 분석을 수행해 보자.

anova_result <- aov(body_mass_g ~ species, data = penguins)
summary(anova_result)

             Df    Sum Sq  Mean Sq F value Pr(>F)    
species       2 146864214 73432107   343.6 <2e-16 ***
Residuals   339  72443483   213698                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
2 observations deleted due to missingness

통계적으로 유의미한 차이가 있는 것으로 보인다. 이제 Tukey’s HSD를 사용하여 이 차이에 어떤 그룹간의 차이에 의한 것인지 확인할 수 있다. 이 방법은 다음과 같은 방법으로 계산되는 HSD 값을 사용하는데, 이 값고 각 그룹간의 평균 차이를 비교하여 통계적 유의성을 판단한다.

\[ \text{HSD} = q_{\alpha}(k, \text{df}{\text{within}}) \cdot \sqrt{\frac{\text{MS}{\text{within}}}{n}} \]

• \(q_{\alpha}(k, \text{df}_{\text{within}})\): Studentized Range Distribution에서 계산되는 임계값
• \(\text{MS}_{\text{within}}\): 그룹내 평균 제곱합 (Mean Square Within)
• \(n\): 그룹당 관측치의 수(같다고 가정)

베이스 R에서는 TukeyHSD 함수를 사용하여 Tukey’s HSD를 수행할 수 있다.

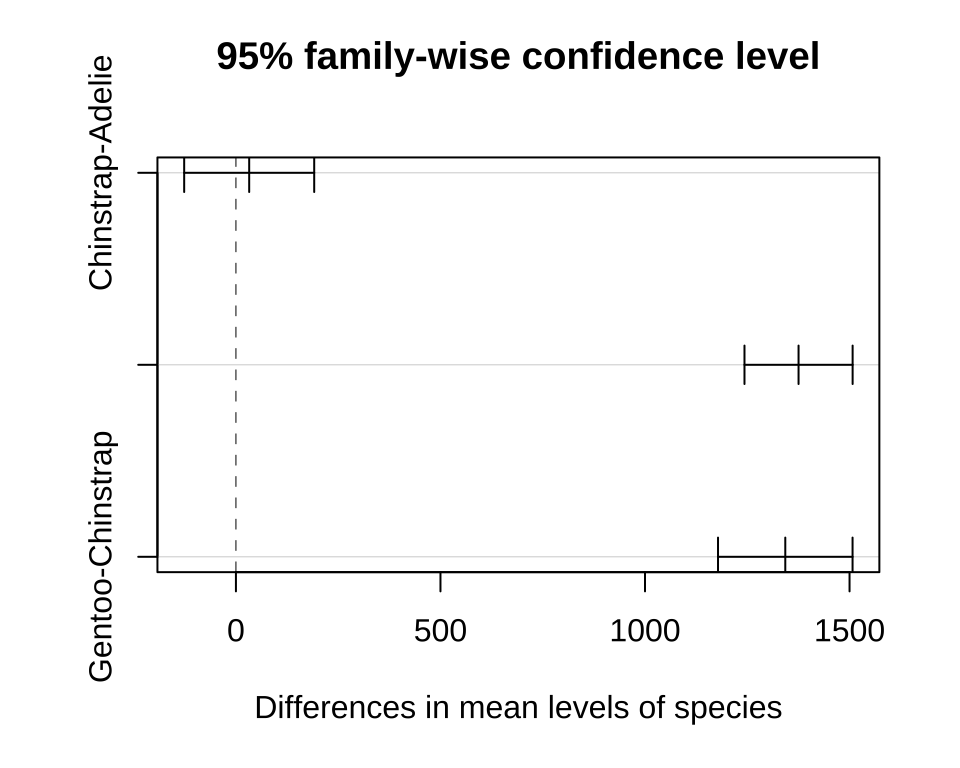
TukeyHSD(anova_result)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = body_mass_g ~ species, data = penguins)

$species
                       diff       lwr       upr     p adj
Chinstrap-Adelie   32.42598 -126.5002  191.3522 0.8806666
Gentoo-Adelie    1375.35401 1243.1786 1507.5294 0.0000000
Gentoo-Chinstrap 1342.92802 1178.4810 1507.3750 0.0000000

plot(TukeyHSD(anova_result))

결과를 보면 Chinstrap penguin과 Adelie penguin 간에는 차이가 없고, Gentoo penguin과 Chinstrap penguin 간에는 차이가 있으며, Gentoo penguin과 Adelie penguin 간에는 차이가 있는 것으로 보인다.

Tukey’s HSD 결과 해석 방법

• ChatGTP 질문: “Tukey’s HSD test 결과를 논문에 보고하려고 어떻게 하는 것이 좋을까요?”, 다음과 같은 답변을 얻었다.

---

Tukey’s HSD (Honest Significant Difference) test 결과를 논문에 보고할 때는 다음과 같은 형식을 사용할 수 있습니다. 이 형식은 독자가 결과를 명확하게 이해할 수 있도록 필요한 정보를 포함합니다.

1. 검정의 목적: Tukey’s HSD test가 수행된 이유를 간단히 설명합니다.
2. 검정 결과: 각 그룹 간의 평균 차이와 그에 대한 통계적 유의성을 보고합니다.
3. p-value: 각 비교에 대한 p-value를 명시합니다.
4. 결론: 어떤 그룹 간에 유의미한 차이가 있는지 설명합니다.

예시:

“Tukey’s HSD test was conducted to determine which specific groups differed in terms of body mass among the penguin species. The results indicated that there was no significant difference between Chinstrap and Adelie penguins (p = 0.45), while significant differences were found between Gentoo and Chinstrap penguins (p < 0.01), and between Gentoo and Adelie penguins (p < 0.01). These findings suggest that Gentoo penguins have a significantly different body mass compared to the other two species.”

이 예시에서:

• 각 그룹 간의 비교 결과와 p-value를 명시합니다.
• 유의미한 차이가 있는 그룹 간의 관계를 설명합니다.

이 형식을 참고하여, 실제 데이터에 맞게 그룹 간의 비교 결과와 p-value를 대체하여 작성하시면 됩니다.

본페로니 보정(Bonferroni correction) 방법도 있다. 이 방법은 각 비교 검정의 임계값을 조정하여 1종 오류를 통제하는 방법이다. 예를 들어, 21개의 비교 검정을 수행할 때, 각 비교 검정의 임계값을 0.05 / 21로 조정하여 1종 오류를 통제한다. 이것은 R에서 pairwise.t.test() 함수를 사용하여 수행할 수 있다.

pairwise.t.test(
    penguins$body_mass_g,
    penguins$species,
    p.adjust.method = "bonferroni"
)

    Pairwise comparisons using t tests with pooled SD 

data:  penguins$body_mass_g and penguins$species 

          Adelie Chinstrap
Chinstrap 1      -        
Gentoo    <2e-16 <2e-16   

P value adjustment method: bonferroni 

32.8 정리

이 장에서는 분산 분석에서 제곱합(sum of squares)과 자유도(degrees of freedom)의 개념에 대해 설명했다. 제곱합은 데이터의 변동성을 측정하는 데 사용되며, 자유도는 통계적 추정에서 독립적으로 변할 수 있는 값의 개수를 의미한다. 또한, 다중 비교(multiple comparison)를 통해 그룹 간의 차이를 검정하는 방법에 대해서도 알아보았다.

Lazic, Stanley E. 2016. Experimental Design for Laboratory Biologists. Cambridge University Press.