28  P-value의 의미 (with infer package)

가설 검정(hypothesis testing) 또는 Null Hypotheisis Significance Test에서 p-값을 보고 어떤 결정을 내린다. 이 장에서는 p-값의 의미와 해석에 대해 알아보려고 한다. 이런 p-값은 통계학에서 매우 중요한 것인데, 개념을 오인하기 쉽기로도 악명이 높다. 어떤 책에 나온 퀴즈를 번역한 것이다(Lazic 2016). 어느 것이 정답일까?

통계학 퀴즈 p-값 0.05가 당신에게 말하는 것은 …
  1. 귀무가설(H0)이 참일 확률 (즉, 효과가 없을 가능성이 5%)
  2. 대립가설(H1)이 참일 확률이 95% (그래서 효과가 실제할 확률이 높다.)
  3. 재현될 확률이 95% 이상이다.
  4. 결과가 거짓 양성일 확률이 5%이다.
  5. 효과의 크기에 관한 어떤 것; 낮은 p-값은 큰 효과를 시사
  6. 귀무가설이 참이라고 가정했을 때, 이때 얻어지는 결과보다 같거나 또는 더 극단적인 결과를 얻을 확률
  7. 위 목적들의 일부 조합 (어떤 내용인지 명시하세요).

이 장에서는 infer 패키지를 사용하여 p-값을 계산하는 방법을 알아보고, p-값의 의미와 해석에 대해 설명한다. infer 패키지는 R에서 통계적 가설 검정을 수행하는 데 유용한 도구를 제공한다. 이 패키지를 사용하면 p-값을 쉽게 계산하고, 이를 통해 귀무가설을 검정할 수 있다. 이 파트의 후반분에서 “가설 검정” 방법론이 비교적 일반적인 원리에 따른다는 것을 이해하게 되면 infer 패키지를 더 잘 사용할 수 있을 것이다.

다만, 여기서는 p-값의 의미와 해석에 중점을 두고 설명한다.

28.1 t-검정

28.1.1 전통적인 방법: 마치 매뉴얼에 따라서 하는 것처럼

29 장에서 t-검정(t-test)에 대해 설명했다. t-검정은 두 집단의 평균을 비교하는 통계적 방법이다. 이때 p-값은 두 집단의 평균 차이가 우연에 의한 것인지, 아니면 실제로 차이가 있는지를 판단하는 데 사용된다.

29 장에서 설명하는 바와 같이 방의 길이를 측정한 roomwidth 데이터셋을 사용한다.

library(HSAUR2)
library(tidyverse)
data("roomwidth", package = "HSAUR2")
glimpse(roomwidth)
Rows: 113
Columns: 2
$ unit  <fct> metres, metres, metres, metres, metres, metres, metres, metres, …
$ width <dbl> 8, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 12, 12, 13, 13, 13…

이 데이터셋은 방의 너비를 피트(feet)와 미터(meters) 단위로 측정한 것이다. 이 데이터를 사용하여 두 집단(피트와 미터)의 평균 차이를 검정하려고 하는데, 먼저 두 집단의 평균을 비교하기 위해 데이터를 변환한다. 1미터는 3.28피트이므로, 방의 너비를 하나의 단위로 맞추어 converted라는 새로운 변수를 만든다.

df <- roomwidth |>
    mutate(
        converted = ifelse(
            unit == "feet", 1 * width, 3.28 * width
        )
    )

전통적인 방법으로 t-검정을 수행하려면 t.test() 함수를 사용하고 p-값을 확인한다. 이때 귀무가설은 두 집단의 평균이 동일하다는 것이다. 즉, p-값이 0.05보다 작으면 귀무가설을 기각하고, 두 집단의 평균이 통계적으로 유의미하게 다르다고 판단한다.

t_test_result <- t.test(
    converted ~ unit,
    data = df,
    var.equal = TRUE
)
t_test_result

    Two Sample t-test

data:  converted by unit
t = -2.6147, df = 111, p-value = 0.01017
alternative hypothesis: true difference in means between group feet and group metres is not equal to 0
95 percent confidence interval:
 -15.572734  -2.145052
sample estimates:
  mean in group feet mean in group metres 
            43.69565             52.55455

계산된 p-값이 0.0102이므로, 0.05보다 작다. 따라서 귀무가설을 기각하고, 두 집단의 평균이 통계적으로 유의미하게 다르다고 결론 내린다.

28.1.2 infer 패키지: 가설 검정 방법론에 따라서

infer 패키지를 사용하여 p-값을 계산하는 방법을 보자.

먼저 우리는 우리가 관찰한 데이터에서 통계량을 계산한다.

library(infer)
observed_stat <- df |>
    specify(converted ~ unit) |>
    calculate(stat = "t", order = c("feet", "metres"))
observed_stat
Response: converted (numeric)
Explanatory: unit (factor)
# A tibble: 1 × 1
   stat
  <dbl>
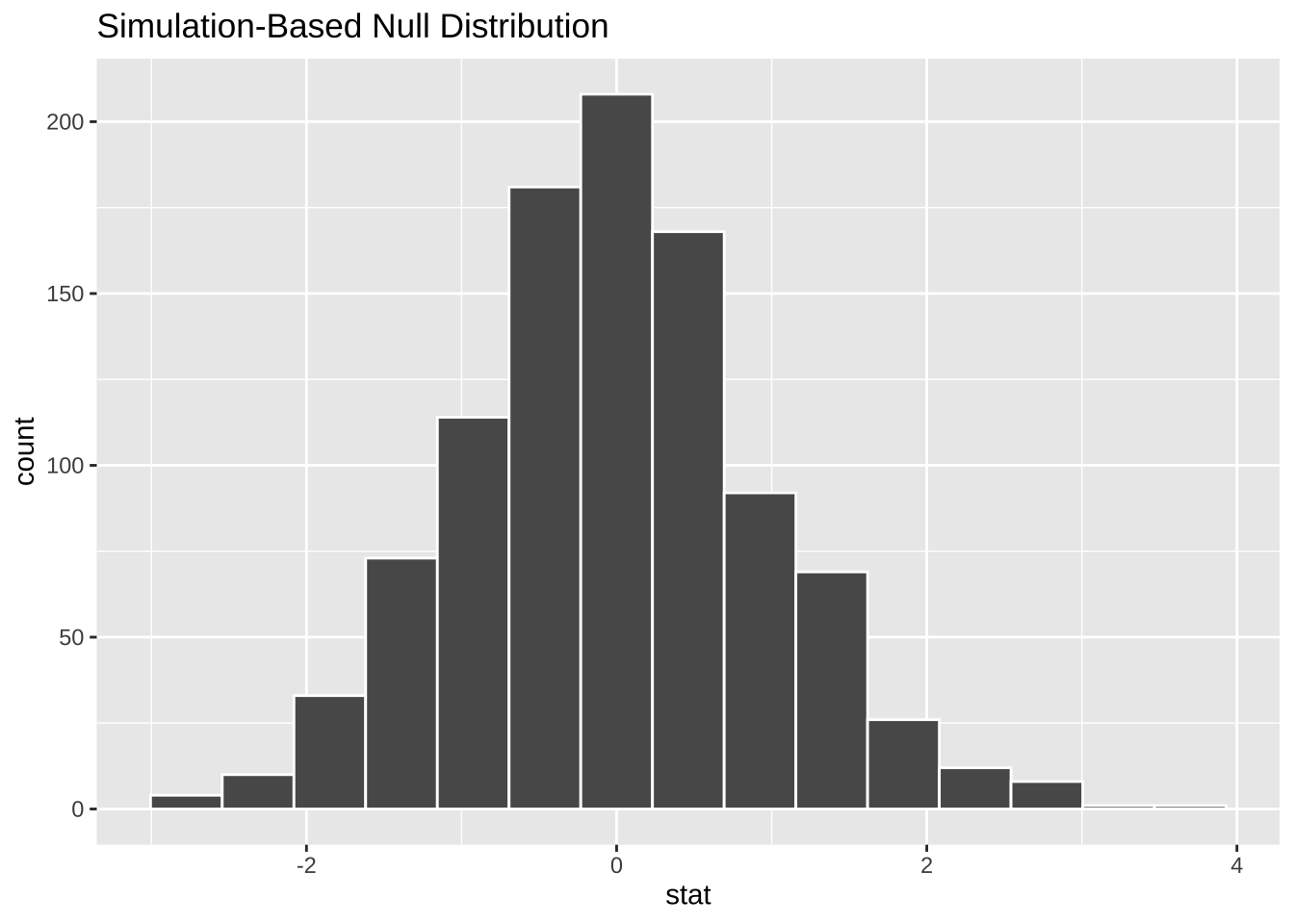
1 -2.31

다음은 두 집단의 평균이 동일하다는 귀무가설이 참이라고 가정하고, 이때의 분포를 시뮬레이션한다. 이때 hypothesize() 함수를 사용하여 귀무가설을 설정하고, generate() 함수를 사용하여 시뮬레이션을 수행하고(이 경우에는 1000번의 반복을 수행한다), calculate() 함수를 사용하여 각 반복에서 t-통계량을 계산한다. 이 통계량이 분포가 귀무가설이 참일 때의 분포를 나타낸다.

null_dist <- df |>
    specify(converted ~ unit) |>
    hypothesize(null = "independence") |>
    generate(reps = 1000, type = "permute") |>
    calculate(stat = "t", order = c("feet", "metres"))

infer 패키지의 visualize() 함수를 사용하여 이 분포를 시각화하고, shade_p_value() 함수를 사용하여 관찰된 통계량에 해당하는 p-값을 음영 처리한다.

library(showtext)
showtext_auto()
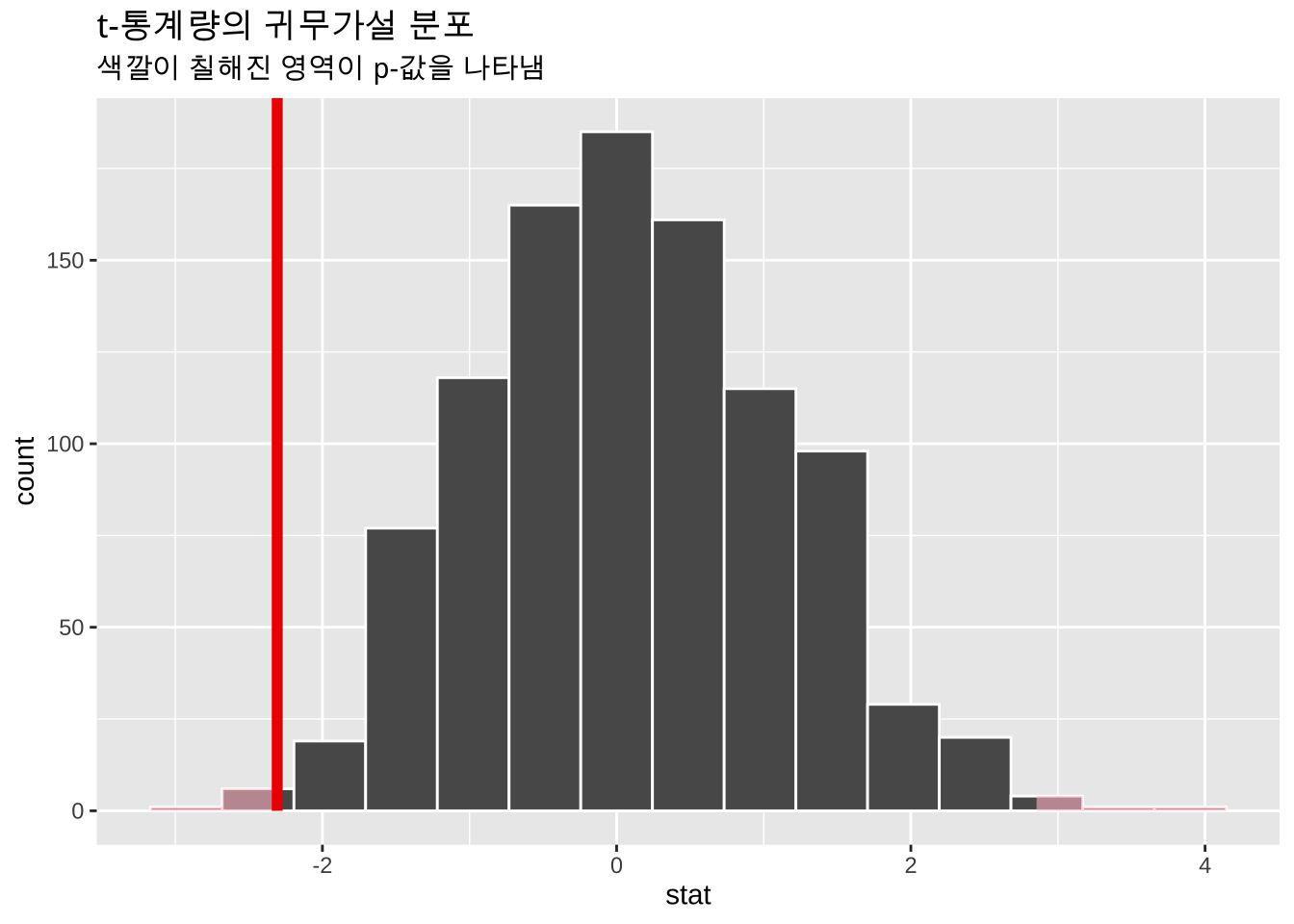
visualize(null_dist) +
    shade_p_value(obs_stat = observed_stat, direction = "two-sided") +
    labs(
        title = "t-통계량의 귀무가설 분포",
        subtitle = "색깔이 칠해진 영역이 p-값을 나타냄"
    )

이 그래프에서 음영 처리된 영역이 p-값을 나타낸다. p-값은 관찰된 t-통계량보다 같거나 더 극단적인 t-통계량을 얻을 확률이다.

이제 p-값을 계산해 보자. infer 패키지의 get_p_value() 함수를 사용하여 p-값을 계산할 수 있다. 이 함수는 관찰된 통계량과 귀무가설 분포를 인자로 받아 p-값을 반환한다.

p_value <- null_dist |>
    get_p_value(obs_stat = observed_stat, direction = "two-sided")
p_value
# A tibble: 1 × 1
  p_value
    <dbl>
1   0.006

여기서 계산한 p-값은 전통적인 방법으로 계산한 p-값과 거의 동일하다. 전통적인 방법은 수학적인 공식에 따른 것이고, infer 패키지는 시뮬레이션을 통해 p-값을 계산하기 때문에 약간은 차이가 있을 수 있다. 그러나 두 방법 모두 p-값의 의미는 동일하다.

28.2 p-값의 의미와 해석

위 infer 패키지를 사용한 방법에서 p-값은 어떻게 계산되고 있는지 다시 살펴보자.

먼저 p-값이 어디에서 계산되고 있는가?

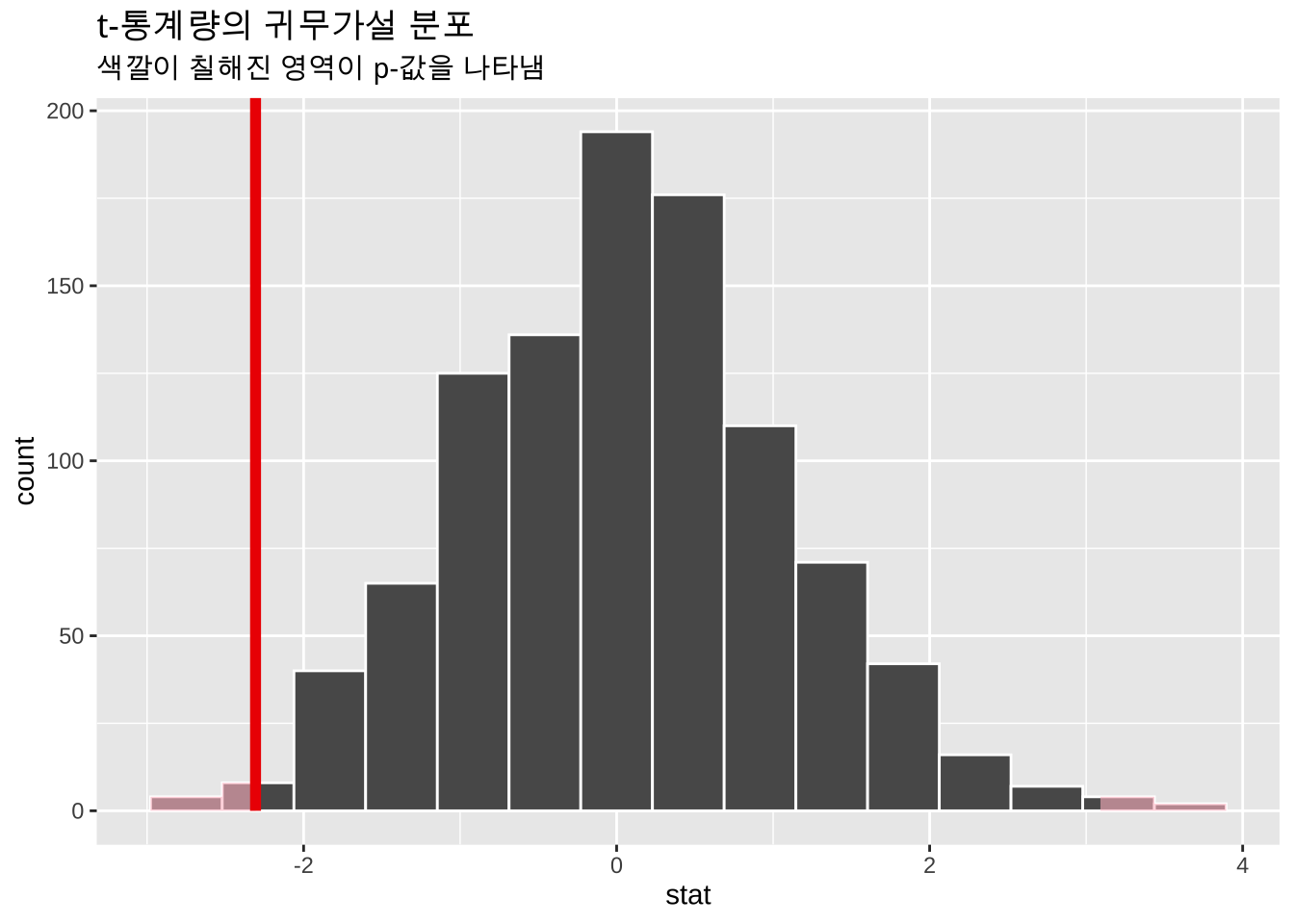
visualize(null_dist) +
    shade_p_value(obs_stat = observed_stat, direction = "two-sided") +
    labs(
        title = "t-통계량의 귀무가설 분포",
        subtitle = "색깔이 칠해진 영역이 p-값을 나타냄"
    )

  • 일단 p-값은 어떤 확률 분포 곡선의 아래 면적을 나타내는 확률(probability) 값이다. 그 면적은 관찰된 통계량보다 같거나 더 극단적인 통계량을 얻을 확률을 나타낸다.

  • 그리고 p-값이 결정되는 것은 우리가 관찰할 데이터에서 얻어진 통계량(observed statistic)에 따라서 달라지는 값이다. 강조하고자 하는 것은 우리가 설정한 가설의 참과 거짓을 확률이 아니라는 것이다. 가설의 확률이 아니라 관찰된 통계량(데이터)의 확률인 것이다.

그리고 우리가 p-값을 어떤 확률 분포에서 계산하고 있는가?

  • 다음에서 보는 바와 같이 p-값이 얻어지는 확률 분포는 귀무가설 참이라고 가정했을 때 얻어지는 통계량의 분포이다.
null_dist <- df |>
    specify(converted ~ unit) |>
    hypothesize(null = "independence") |>
    generate(reps = 1000, type = "permute") |>
    calculate(stat = "t", order = c("feet", "metres"))
visualize(null_dist)

이제 p-값의 의미를 알았으니 문제를 다시 살펴보자. 정답이 f임을 이해할 수 있을 것이다(모르겠으면 다시 위 내용을 읽어보자).

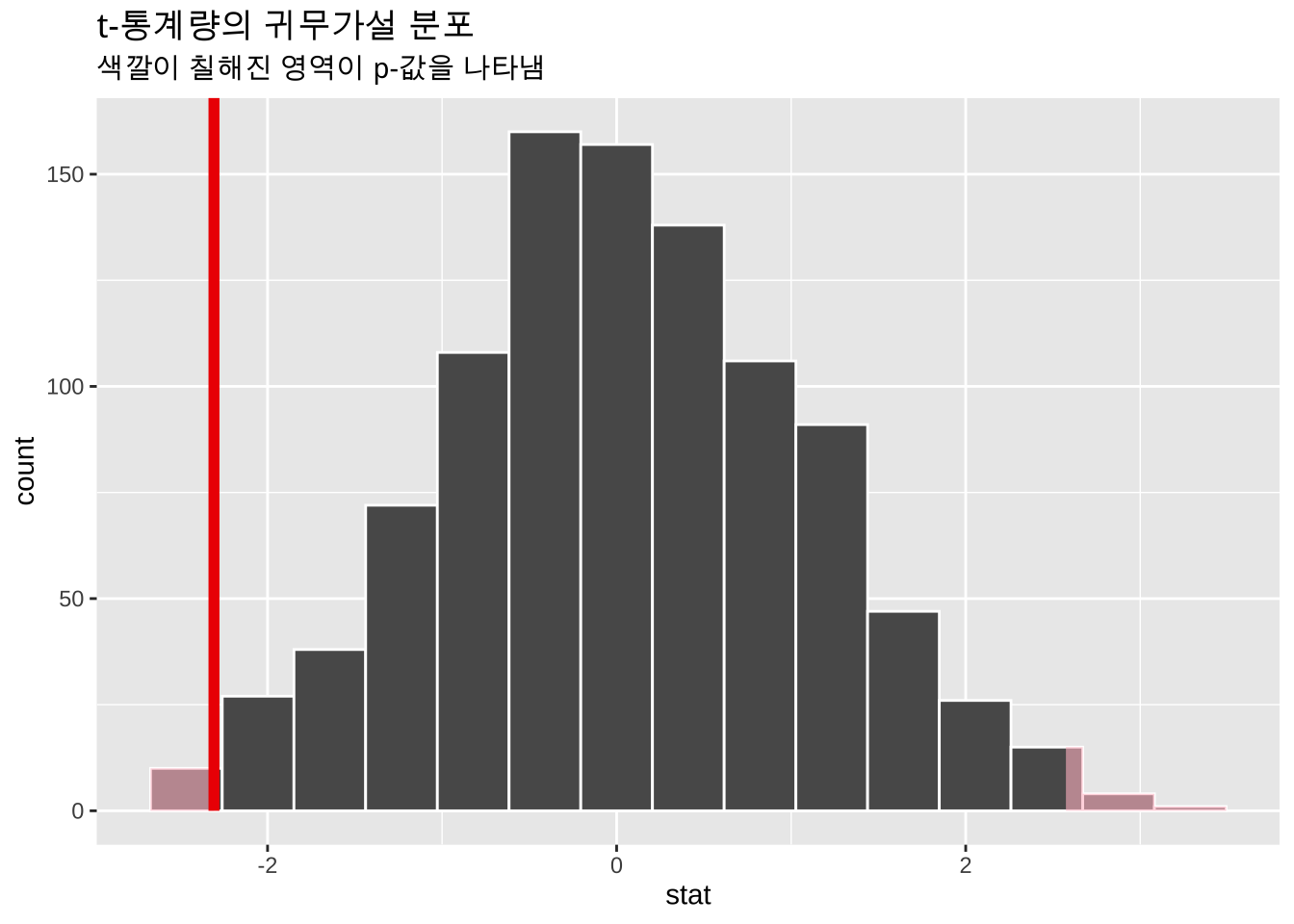
visualize(null_dist) +
    shade_p_value(obs_stat = observed_stat, direction = "two-sided") +
    labs(
        title = "t-통계량의 귀무가설 분포",
        subtitle = "색깔이 칠해진 영역이 p-값을 나타냄"
    )

통계학 퀴즈 p-값 0.05가 당신에게 말하는 것은 …
  1. 귀무가설(H0)이 참일 확률 (즉, 효과가 없을 가능성이 5%)
  2. 대립가설(H1)이 참일 확률이 95% (그래서 효과가 실제할 확률이 높다.)
  3. 재현될 확률이 95% 이상이다.
  4. 결과가 거짓 양성일 확률이 5%이다.
  5. 효과의 크기에 관한 어떤 것; 낮은 p-값은 큰 효과를 시사
  6. 귀무가설이 참이라고 가정했을 때, 이때 얻어지는 결과보다 같거나 또는 더 극단적인 결과를 얻을 확률
  7. 위 목적들의 일부 조합 (어떤 내용인지 명시하세요).

즉, p-값은 귀무가설이 참이라고 가정했을 때, 관찰된 통계량보다 같거나 더 극단적인 통계량을 얻을 확률이다. 따라서 p-값이 작다는 것은 관찰된 통계량이 귀무가설 하에서 발생하기 어려운 값이라는 것을 의미한다.

28.3 정리

아마도 논문 등을 쓸 때는 전통적인 방법으로 p-값을 계산할 것이다. 그렇더라도 p-값의 개념이 흔들릴 때는 infer 패키지를 떠올릴 필요가 있다. 그럼 헷갈리지 않을 것이다.