33 일원 분산 분석(One-way ANOVA)
32장에서 분산분석의 기본 원리를 보았다. 이 장에서는 일원 분산분석(one-way ANOVA)에 대해 알아보자.
- 하나의 양적 종속 변수
- 하나의 범주형 독립 변수
예를 들어, 세 가지 다른 치료 방법이 환자의 혈압에 미치는 영향을 비교하고자 할 때, 치료 방법이 독립 변수이고 혈압이 종속 변수(dependent variable)가 된다.
먼저 분산분석의 가정들에 대해 알아보고 난 후 실제 R 코드를 통해 분산분석을 수행하는 방법을 보자.
33.1 등분산 가정(homogeneity of variance, homoscedasticity)
교과서에 따르면 ANOVA는 등분산 가정을 전제로 한다. 그 의미를 알아보자.
왜 그럴까? ANOVA는 그룹 간의 평균 차이를 검정하는 방법인데 F-통계량을 사용한다. F-통계량은 다음과 같이 계산된다.
\[ F = \frac{SSg/df1}{SSr/df2}=\frac{MS_{\text{between}}}{MS_{\text{within}}} \]
4 개의 그룹이 있다고 가정해 보자. 3개의 그룹은 분산이 비슷한데, 1개의 그룹은 분산이 크게 다르다고 가정해 보자. 이 경우 F-통계량은 이 크게 다른 1개의 그룹에 의해 크게 영향을 받게 된다. 즉, 분산이 다른 그룹이 존재하면 F-통계량이 왜곡되어 ANOVA의 결과가 신뢰할 수 없게 된다. 어떻게 보면 Simpson의 역설(Simpson’s paradox)과 비슷하다.
33.1.1 등분산 가정을 검정
등분산 가정을 검정하는 방법은 여러 가지가 있다. 가장 많이 사용되는 방법은 Levene’s test와 Bartlett’s test이다. 먼저 시각화를 통해서 각 그룹의 분산이 비슷한지 확인할 수 있다. 예를 들어, ggplot2 패키지를 사용하여 상자 그림(boxplot)을 그려보자. palmerpenguins 패키지에 있는 펭귄 데이터를 사용하여 각 종별 몸무게의 분포를 시각화해 보자.
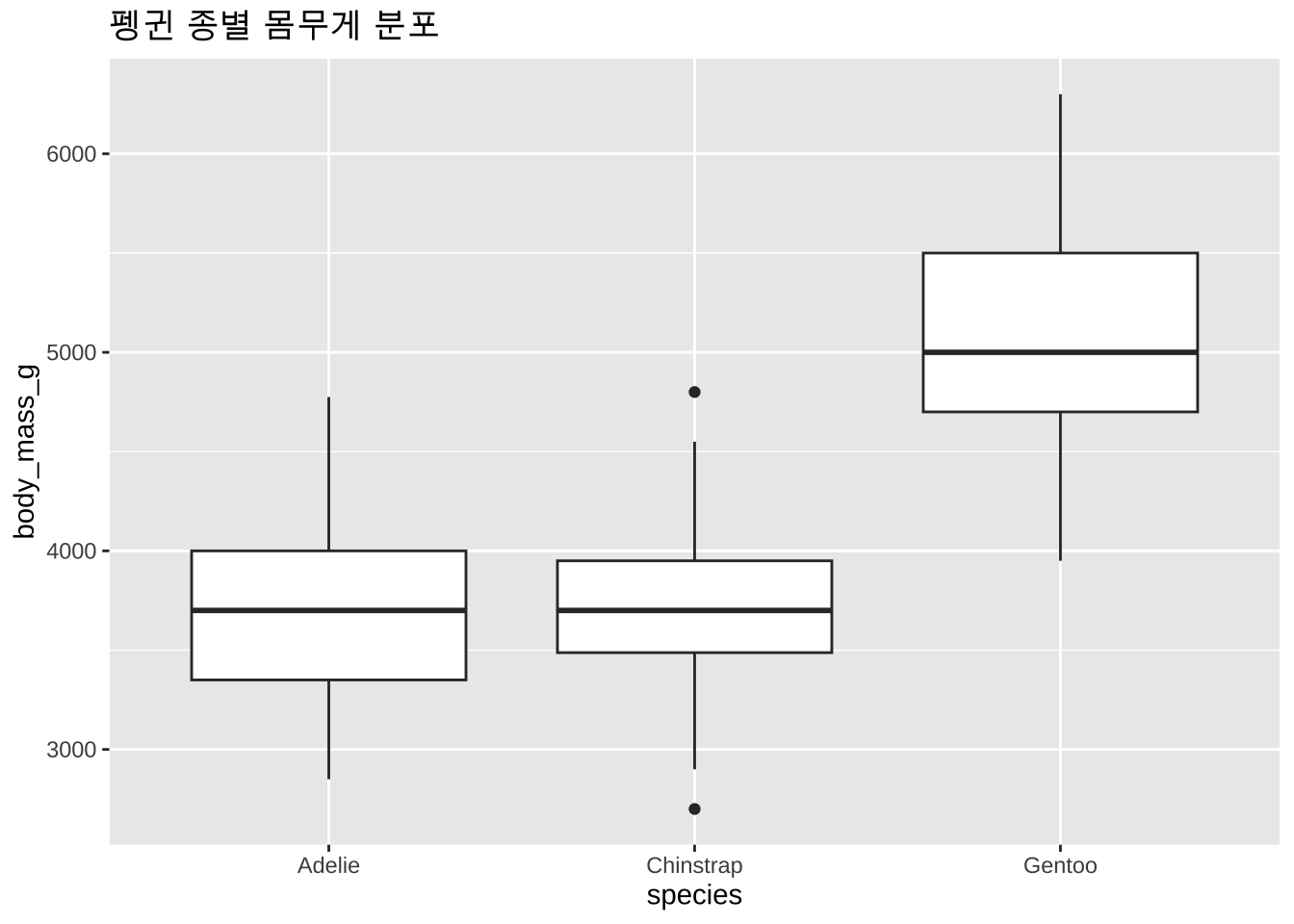
먼저 박스 플롯을 보자. 박스 플롯은 상자의 중앙값, 사분위수, 이상치 등을 시각적으로 보여준다. 박스 플롯을 통해 각 그룹의 분포와 분산에 대해 감을 잡을 수 있다. 박스의 높이가 얼마나 같은지 보면 될 것이다.
penguins %>%
ggplot(aes(x = species, y = body_mass_g)) +
geom_boxplot() +
labs(title = "펭귄 종별 몸무게 분포")Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_boxplot()`).히스토그램 또는 밀도 그래프를 사용하여 각 그룹의 분포를 시각적으로 확인할 수도 있다. 밀도 그래프는 각 그룹의 분포를 부드럽게 나타내어 분산을 비교하는 데 유용하다. 이 경우에는 분포의 폭이 얼마나 비슷한지 확인하면 된다.
penguins %>%
ggplot(aes(fill = species, x = body_mass_g)) +
geom_density(alpha=0.5) +
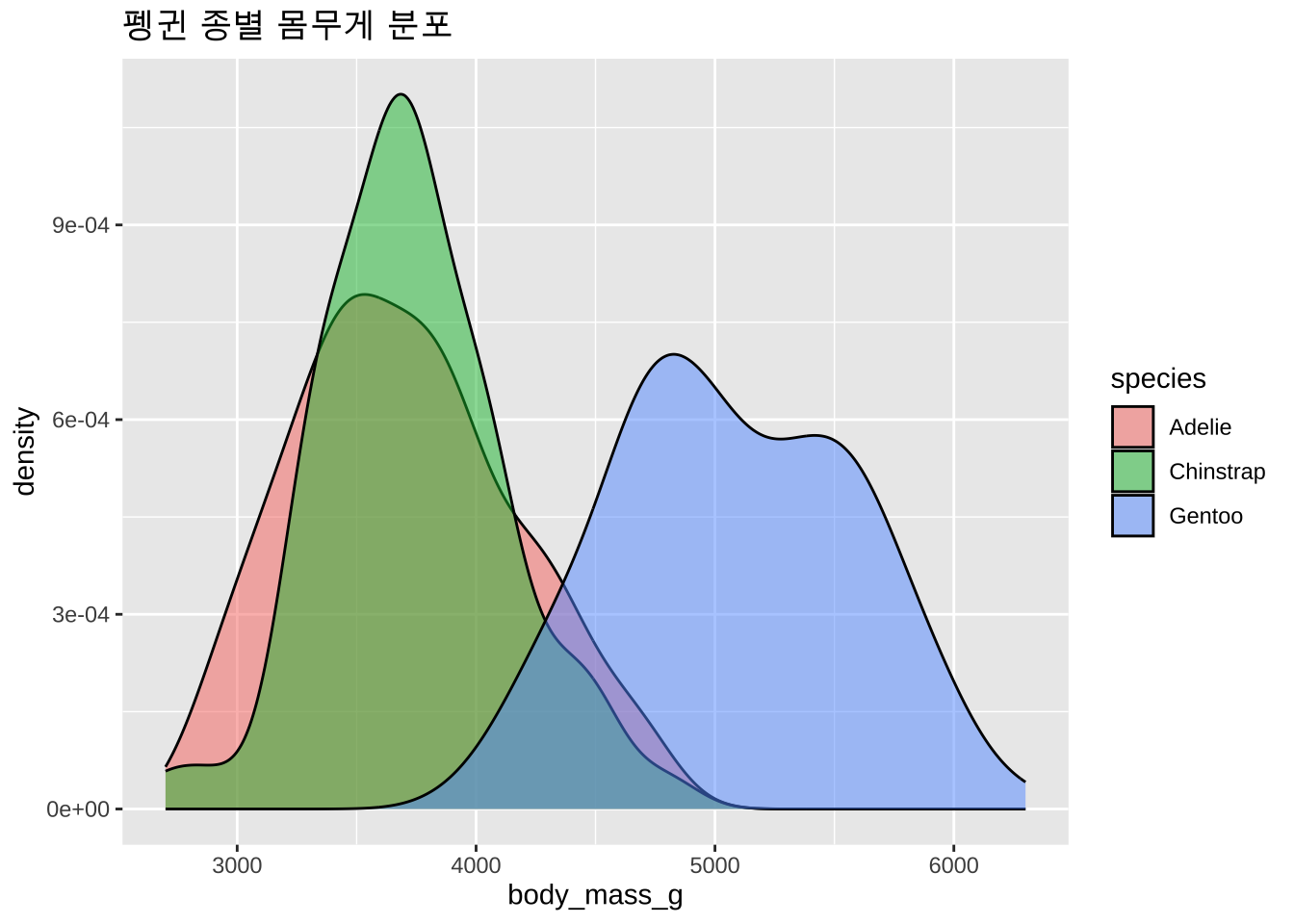
labs(title = "펭귄 종별 몸무게 분포")Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_density()`).시각적으로 보면 Gentoo 펭귄의 몸무게 분포가 다른 종들에 비해 더 넓은 편이다. 즉, Gento 펭귄의 몸무게 분산이 다른 종들에 비해 더 크다는 것을 알 수 있다.
이제 Levene’s test를 수행해 보자. Levene’s test는 각 그룹의 분산이 동일한지 검정하는 방법이다. car 패키지의 leveneTest() 함수를 사용하여 Levene’s test를 수행할 수 있다.
library(car)
leveneTest(body_mass_g ~ species, data = penguins) |>
broom::tidy()# A tibble: 1 × 4
statistic p.value df df.residual
<dbl> <dbl> <int> <int>
1 5.12 0.00645 2 339결과를 보면 p-value가 0.05보다 작으므로, 등분산 가정이 충족되지 않는다는 것을 알 수 있다.
또다른 방법으로 Bartlett’s test가 있다. 이것도 정규성을 가정하는 등분산 검정 방법인데, 비모수적인 방법이며 데이터가 정규성을 만족할 때 사용한다. bartlett.test() 함수를 사용하여 Bartlett’s test를 수행할 수 있다.
bartlett.test(body_mass_g ~ species, data = penguins) |>
broom::tidy()# A tibble: 1 × 4
statistic p.value parameter method
<dbl> <dbl> <dbl> <chr>
1 5.99 0.0500 2 Bartlett test of homogeneity of variances이 경우에는 p-value가 거의 경계에 걸쳐 있다.
결과가 이렇게 나오면 그룹들간의 등분산을 가정하는 일반적인 ANOVA 분석을 수행한다면 결과가 왜곡될 수 있음을 의미한다. 이런 경우에는 Welch’s ANOVA를 사용하는 것이 권고되며, 베이스 R의 oneway.test() 함수를 사용하는데 아래 예시와 같이 var.equal = FALSE 인자를 사용하여 분산이 같다는 조건을 무시하게 한다.
oneway.test(body_mass_g ~ species, data = penguins, var.equal = FALSE) |>
broom::tidy()# A tibble: 1 × 5
num.df den.df statistic p.value method
<dbl> <dbl> <dbl> <dbl> <chr>
1 2 189. 318. 3.09e-61 One-way analysis of means (not assuming equa…33.1.2 잔차의 정규성 가정(normality assumption)
교과서에 따르면 ANOVA는 정규성 가정을 전제로 한다. 그 의미를 알아보자.
왜 이런 가정이 필요할까? ANOVA에서 사용되는 F-통계량과 F-분포는 이러한 가정에 바탕을 두고 만들어진 도구이기 때문이다.
앞에 penguins 데이터에 대해 ANOVA를 수행했을 때의 잔차(residual)를 먼저 확인해 보자. 잔차는 모델의 예측값과 실제 관측값의 차이로, ANOVA 모델을 적합한 후 augment() 함수를 사용하여 잔차를 추출할 수 있다.
df <- penguins |>
select(species, body_mass_g)
result <- aov(body_mass_g ~ species, data = df) |>
broom::augment() Warning: The `augment()` method for objects of class `aov` is not maintained by the broom team, and is only supported through the `lm` tidier method. Please be cautious in interpreting and reporting broom output.
This warning is displayed once per session.result# A tibble: 342 × 9
.rownames body_mass_g species .fitted .resid .hat .sigma .cooksd
<chr> <int> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 3750 Adelie 3701. 49.3 0.00662 463. 0.0000255
2 2 3800 Adelie 3701. 99.3 0.00662 463. 0.000103
3 3 3250 Adelie 3701. -451. 0.00662 462. 0.00213
4 5 3450 Adelie 3701. -251. 0.00662 463. 0.000658
5 6 3650 Adelie 3701. -50.7 0.00662 463. 0.0000269
6 7 3625 Adelie 3701. -75.7 0.00662 463. 0.0000599
7 8 4675 Adelie 3701. 974. 0.00662 460. 0.00994
8 9 3475 Adelie 3701. -226. 0.00662 463. 0.000533
9 10 4250 Adelie 3701. 549. 0.00662 462. 0.00316
10 11 3300 Adelie 3701. -401. 0.00662 462. 0.00168
# ℹ 332 more rows
# ℹ 1 more variable: .std.resid <dbl>이 결과에서 .resid 열이 잔차이다. 실제 값 body_mass_g에서 예측값(.fitted)을 뺀 값이다. 이 값들이 정규분포를 따라야 한다는 가정인 것이다.
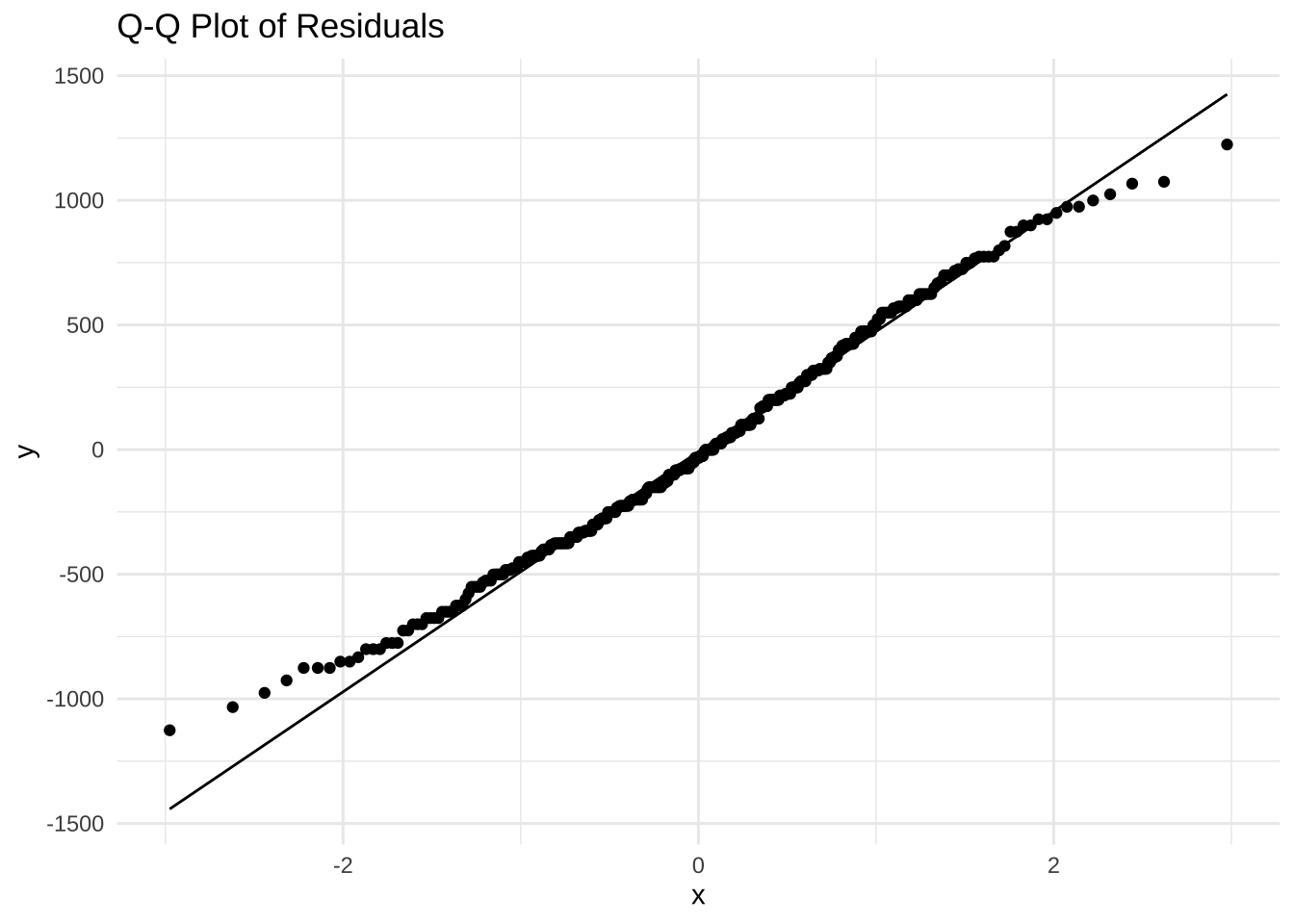
잔차의 정규성을 시각적으로 확인하기 위해 Q-Q 플롯(Quantile-Quantile Plot)을 그려보자. Q-Q 플롯은 데이터의 분포가 정규분포와 얼마나 유사한지를 시각적으로 보여준다.
result |>
ggplot(aes(sample = .resid)) +
stat_qq() +
stat_qq_line() +
labs(title = "Q-Q Plot of Residuals") +
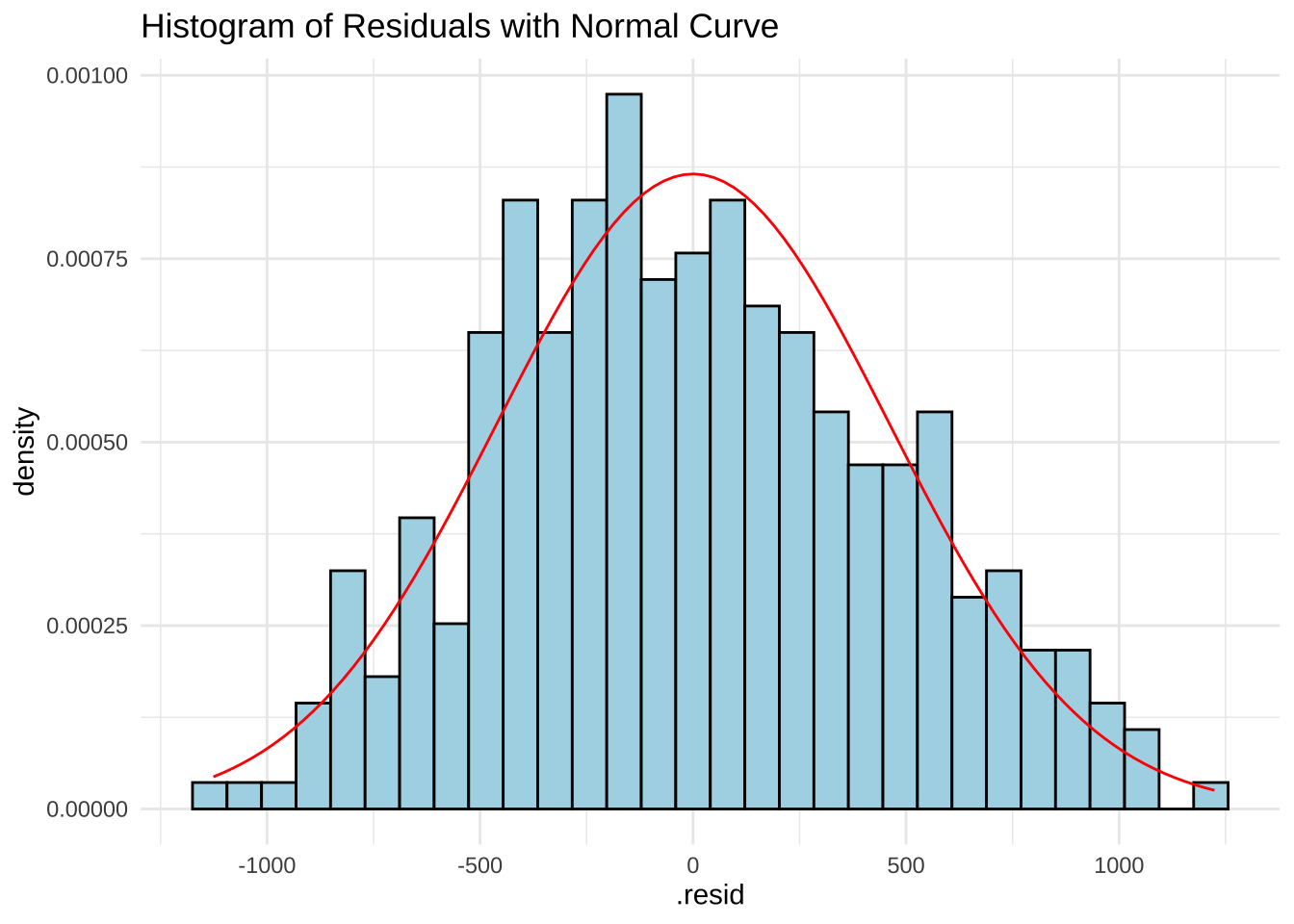
theme_minimal()히스토그램도 그려보자. 히스토그램은 잔차의 분포를 시각적으로 보여준다. 정규분포를 따르는 경우, 히스토그램은 종 모양의 곡선을 나타내야 한다.
result |>
ggplot(aes(x = .resid)) +
geom_histogram(aes(y = ..density..), bins = 30, fill = "lightblue", color = "black") +
stat_function(fun = dnorm, args = list(mean = mean(result$.resid), sd = sd(result$.resid)), color = "red") +
labs(title = "Histogram of Residuals with Normal Curve") +
theme_minimal()Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
ℹ Please use `after_stat(density)` instead.잔차의 정규성을 검정하는 방법으로는 Shapiro-Wilk test가 있다. 이 검정은 잔차가 정규분포를 따르는지 여부를 판단하는 데 사용된다. shapiro.test() 함수를 사용하여 Shapiro-Wilk test를 수행할 수 있다. 귀무가설은 잔차가 정규분포를 따른다는 것이다. 따라서 p-value가 0.05보다 작으면 귀무가설을 기각하고, 잔차가 정규분포를 따르지 않는다고 결론 내린다.
shapiro.test(result$.resid) |>
broom::tidy()# A tibble: 1 × 3
statistic p.value method
<dbl> <dbl> <chr>
1 0.992 0.0512 Shapiro-Wilk normality test위 결과를 보면 p-value가 0.05보다 크므로 잔차가 정규분포를 따른다고 결론 내릴 수 있다.
33.1.3 독립성 가정(independence assumption)
교과서에 따르면 ANOVA는 독립성 가정을 전제로 한다. 그 의미는 다음과 같다.
이 가정은 실험 설계에서 중요한 요소로, 각 그룹의 관측치가 서로 영향을 미치지 않도록 설계되어야 한다. 예를 들어, 동일한 피험자에게서 여러 번 측정한 데이터는 독립적이지 않으므로 ANOVA를 적용할 수 없다. 이 경우에는 반복 측정 ANOVA(repeated measures ANOVA)나 혼합 효과 모델(mixed effects model)을 사용해야 한다.
동물실험을 하는 경우, 같은 어미가 같은 형제들(siblings)을 대상으로 어떤 실험을 할 수 있을 것이다. 이 경우에는 어미가 같은 형제들끼리는 독립적이지 않다. 따라서 ANOVA를 적용할 수 없다.
33.1.4 펭귄 데이터에 대한 ANOVA 가정 결과와 Welch’s ANOVA
위 결과를 요약하면 다음과 같다.
- 등분산 가정: Levene’s test 결과 p-value가 0.05보다 작아 등분산 가정이 충족되지 않음
- 정규성 가정: Shapiro-Wilk test 결과 p-value가 0.05보다 크므로 잔차가 정규분포를 따름
- 독립성 가정: 데이터가 독립적이라고 가정
즉, 등분산 가정을 충족하지 않으므로 이 위에서 본 Welch’s ANOVA를 사용해야 한다. 위에서 본 결과는 다음과 같다.
anova_result <- oneway.test(body_mass_g ~ species, data = penguins, var.equal = FALSE)
anova_result
One-way analysis of means (not assuming equal variances)
data: body_mass_g and species
F = 317.57, num df = 2.00, denom df = 189.48, p-value < 2.2e-1633.2 다중비교
ANOVA를 수행한 후, 그룹 간의 평균 차이가 유의미하다는 결과가 나왔다면, 어떤 그룹 간에 차이가 있는지를 알아보기 위해 다중비교(multiple comparisons)를 수행해야 한다. 보통 Tukey의 HSD(Honestly Significant Difference) 검정을 많이 사용한다. 그런데 이 경우에는 그룹 간의 분산이 다르므로 Tukey의 HSD 검정을 수행할 수 없다. 이 경우에는 다른 방법을 사용해야 한다. Games-Howell 검정도 그런 방법 중 하나이다. rstatix 패키지에 있는 games_howell_test() 함수를 사용하였다.
Attaching package: 'rstatix'The following object is masked from 'package:stats':
filterpenguins |>
games_howell_test(body_mass_g ~ species)# A tibble: 3 × 8
.y. group1 group2 estimate conf.low conf.high p.adj p.adj.signif
* <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <chr>
1 body_mass_g Adelie Chins… 32.4 -109. 174. 8.5 e- 1 ns
2 body_mass_g Adelie Gentoo 1375. 1237. 1514. 0 ****
3 body_mass_g Chinstrap Gentoo 1343. 1189. 1497. 5.85e-14 ****