Rows: 113
Columns: 2
$ unit <fct> metres, metres, metres, metres, metres, metres, metres, metres, …
$ width <dbl> 8, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 12, 12, 13, 13, 13…30 두 연속 변수의 평균 비교: t-test
30.1 독립 2-표본 t-test (independent two-sample t-test)
독립 표본 t-test는 두 개의 독립적인 표본의 평균을 비교하는 통계적 방법이다. 이 방법은 두 집단의 평균이 통계적으로 유의미하게 다른지를 검정하는 데 사용된다. 예를 들어, 두 가지 다른 치료 방법의 효과를 비교하거나, 두 개의 다른 그룹의 성적을 비교할 때 사용할 수 있다.
독립 표본 t-test의 가설은 다음과 같다:
- 귀무가설(H0): 두 표본의 평균이 동일하다. 즉, \(H_0: \mu_1 = \mu_2\).
- 대립가설(H1): 두 표본의 평균이 다르다. 즉, \(H_1: \mu_1 \neq \mu_2\).
독립 표본 t-test를 수행하기 위해서는 다음과 같은 조건을 만족해야 한다:
- 두 표본은 독립적이어야 한다.
- 각 표본은 정규분포를 따라야 한다(normality).
- 두 표본의 분산이 동일해야 한다(등분산, equality of variance).
- 각 표본의 관측치는 서로 독립적(independent)이어야 한다.
- 독립성: 두 표본은 서로 영향을 주지 않아야 한다. 즉, 한 표본의 관측치가 다른 표본의 관측치에 영향을 미치지 않아야 하고, 같은 표본 안에서 관측치 역시 서로 독립적이어야 한다.
- 정규성: 각 표본의 데이터는 정규분포를 따라야 한다. 이는 표본의 크기가 충분히 크면 중심극한정리에 의해 완화될 수 있다.
-
등분산성: 두 표본의 분산이 동일해야 한다. 이는
F-test나Levene's test를 사용하여 검정할 수 있다.
이와 같은 조건을 만족할 때, 독립 표본 t-test의 통계량은 다음과 같이 계산할 수 있다. t-통계량(t-statistic)은 두 표본의 평균이 차이를 표준화한 값이다.
\[ t = \frac{\bar{y_1} - \bar{y_2}}{s\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \]
여기서 \(s\)는 pooled standard deviation(두 집단을 하나로 묶어서 계산한 표준 편차)으로 아래와 같이 계산된다. \[ s = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}} \]
- \(\bar{y_1}\)과 \(\bar{y_2}\)는 각각 두 표본의 평균이다.
- \(s_1\)과 \(s_2\)는 각각 두 표본의 표준편차이다.
- \(n_1\)과 \(n_2\)는 각각 두 표본의 크기이다.
귀무가설이 참이라고 하면 이 t-통계량은 자유도 \(df = n_1 + n_2 - 2\)를 가진 \(t\)-분포를 따른다.
따라서, \(t\)-분포의 누적분포함수(CDF)를 사용하여 p-value를 계산할 수 있다.
만약 두 표본의 분산이 동일하지 않다면, Welch’s t-test를 사용해야 한다. Welch’s t-test는 등분산성을 가정하지 않고, 각 표본의 분산을 따로 계산하여 t-통계량을 계산한다. Welch’s t-test의 t-통계량은 다음과 같이 계산된다. \[
t = \frac{\bar{y_1} - \bar{y_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}
\]
이때, 자유도는 다음과 같이 계산된다.
\[ df = \frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2}{\frac{\left(\frac{s_1^2}{n_1}\right)^2}{n_1 - 1} + \frac{\left(\frac{s_2^2}{n_2}\right)^2}{n_2 - 1}} \]
따라서 알아둘 내용은
- 독립 표본 t-test는 두 개의 독립적인 표본의 평균을 비교하는 통계적 방법으로 표본의 정규성을 가정한다.
- 정규성은
Shapiro-Wilk test를 사용하여 검정할 수 있다. - 정규성을 만족하지 않는 경우, 비모수적 방법인
Wilcoxon Mann-Whitney randk sum test를 사용할 수 있다.
- 정규성은
- 독립 표본 t-통계량을 계산할 때, 등분산을 가정하는 경우와 가정하지 않는 경우가 있다.
- 등분산을 가정하는 경우
t-통계량과 자유도를 계산할 때pooled standard deviation을 사용한다(독립 표본 t-test). - 등분산을 가정하지 않는 경우
t-통계량과 자유도를 계산할 때 각 표본의 표준편차를 따로 사용한다(Welch’s t-test) - 등분산은 아래에서 설명하는 바와 같이
F-test나Levene's test를 사용하여 검정할 수 있다.
- 등분산을 가정하는 경우
- 독립 표본이 아닌 경우, 서로 대응되는 두 표본인 경우(paired samples)에는 대응 표본 t-test를 사용한다. 다음 절에서 다룬다.
- 정규성을 만족하지 않는 경우, 비모수적 방법인
Wilcoxon signed-rank test를 사용할 수 있다.
- 정규성을 만족하지 않는 경우, 비모수적 방법인
30.2 대응 표본 t-test (paired t-test)
대응 표본 t-test는 두 개의 관련된 표본(예: 같은 집단의 전후 측정값)의 평균을 비교하는 통계적 방법이다. 이 방법은 두 표본이 서로 관련되어 있을 때 사용되며, 예를 들어 같은 사람의 치료 전후의 혈압을 비교할 때 사용할 수 있다. 대응 표본 t-test의 가설은 다음과 같다:
- 귀무가설(H0): 두 표본의 평균이 동일하다. 즉, \(H_0: \mu_d = 0\).
- 대립가설(H1): 두 표본의 평균이 다르다. 즉, \(H_1: \mu_d \neq 0\).
대응 표본 t-test를 수행하기 위해서는 다음과 같은 조건을 만족해야 한다:
- 두 표본은 관련되어 있어야 한다.
- 각 표본의 차이는 정규분포를 따라야 한다(normality).
- 각 표본의 관측치는 서로 독립적(independent)이어야 한다.
이와 같은 조건을 만족할 때, 대응 표본 t-test의 통계량은 다음과 같이 계산할 수 있다. t-통계량(t-statistic)은 두 표본의 평균 차이를 표준화한 값이다.
\[ t = \frac{\bar{d}}{s_d / \sqrt{n}} \]
여기서 \(\bar{d}\)는 두 표본의 차이의 평균, \(s_d\)는 두 표본의 차이의 표준편차, \(n\)은 표본의 크기이다. 귀무가설이 참이라고 하면 이 t-통계량은 자유도 \(df = n - 1\)을 가진 \(t\)-분포를 따른다.
30.3 독립 2-표본 t-test 예제: roomwidth
이 예제에서는 두 개의 다른 단위(피트와 미터)로 측정된 방의 너비를 비교한다. HSAUR2 패키지의 roomwidth 데이터를 사용하여, 두 표본의 평균이 통계적으로 유의미하게 다른지를 검정한다.
1미터가 3.28피트이므로, 측정된 방의 너비로 하나의 단위로 맞추어 converted라는 새로운 변수를 만든다.
데이터를 요약해 보면 다음과 같다.
# A tibble: 2 × 4
unit mean sd n
<fct> <dbl> <dbl> <int>
1 feet 43.7 12.5 69
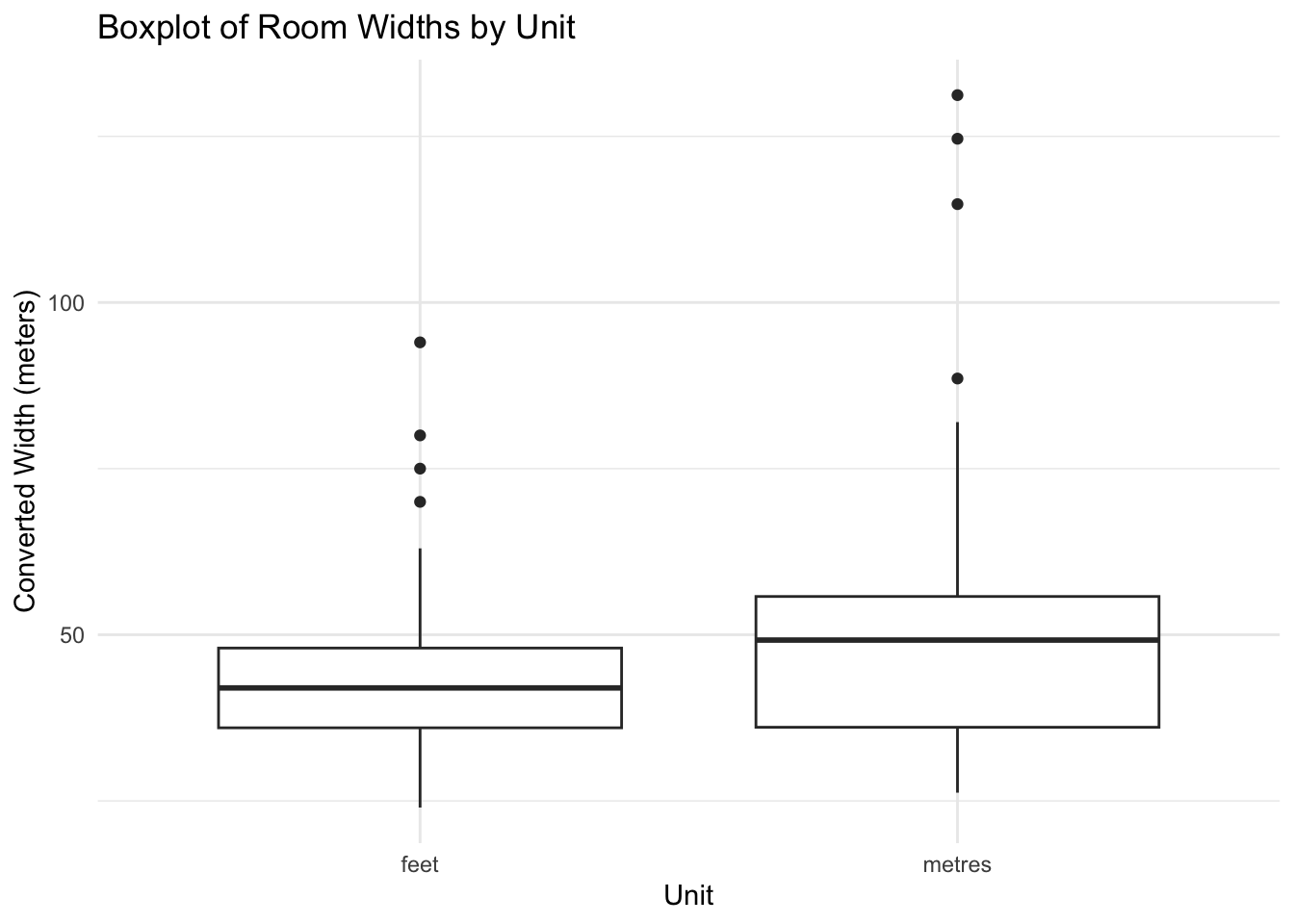
2 metres 52.6 23.4 44박스 플롯을 만들어 보면 다음과 같다.
df |>
ggplot(aes(x = unit, y = converted)) +
geom_boxplot() +
labs(
x = "Unit",
y = "Converted Width (meters)",
title = "Boxplot of Room Widths by Unit"
) +
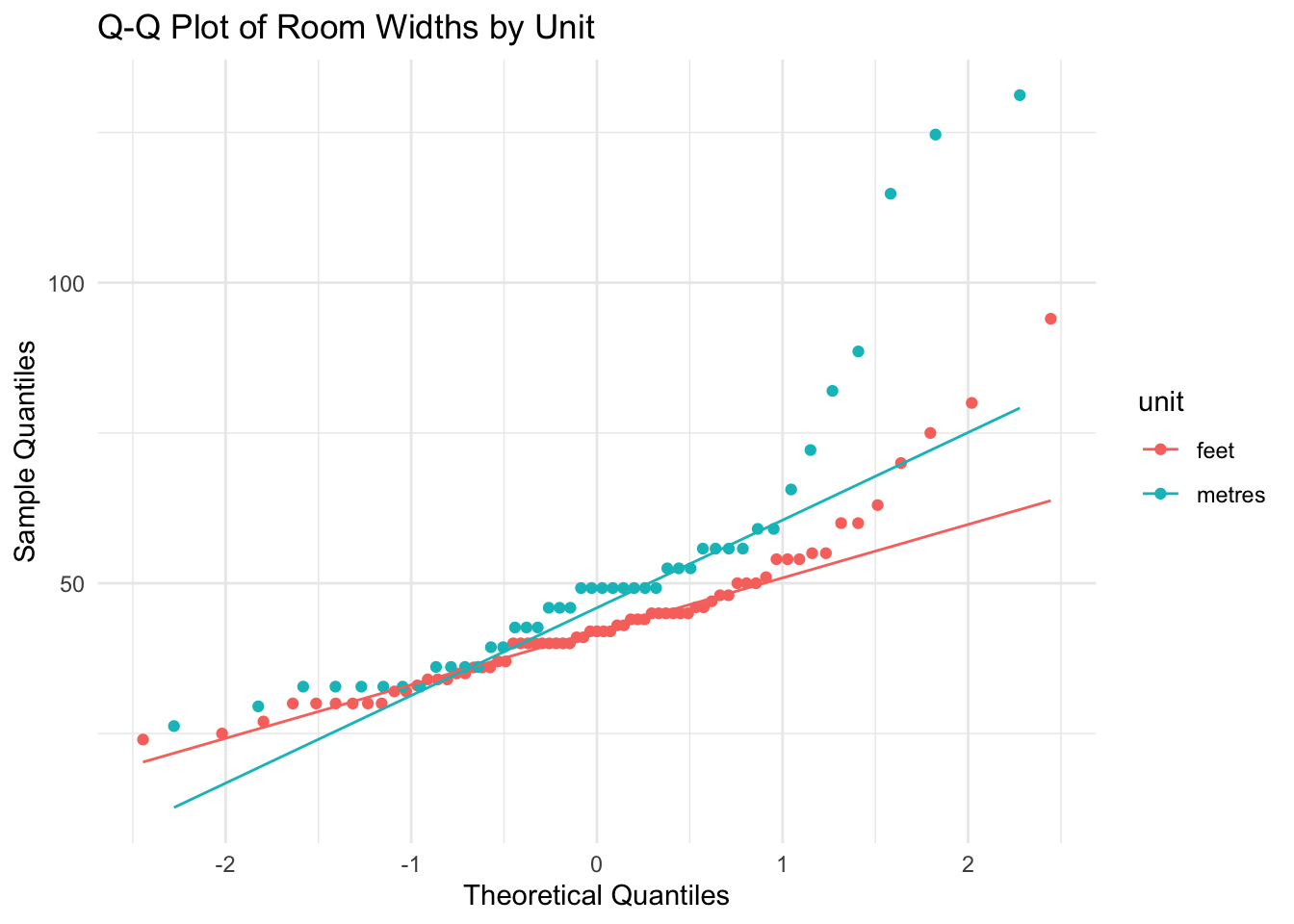
theme_minimal()q-q plot을 사용하여 두 표본의 정규성을 확인할 수 있다.
df |>
ggplot(aes(sample = converted, color = unit)) +
stat_qq() +
stat_qq_line() +
labs(
title = "Q-Q Plot of Room Widths by Unit",
x = "Theoretical Quantiles",
y = "Sample Quantiles"
) +
theme_minimal()이제 가설 검정을 수행해 볼 차례이다. 먼저 가정들을 확인해야 한다.
Shapiro-Wilk test를 사용하여 두 표본의 정규성을 검정할 수 있다.
shapiro_test_result <- df |>
group_by(unit) |>
summarise(
shapiro_p_value = shapiro.test(converted)$p.value
)
shapiro_test_result# A tibble: 2 × 2
unit shapiro_p_value
<fct> <dbl>
1 feet 0.0000131
2 metres 0.000000566Shapiro-Wilk test은 표본이 정규분포를 따른다는 귀무가설을 검정한다. 따라서 이 경우 p-value가 0.05보다 작아서 귀무가설을 기각하고, 두 표본 모두 정규성을 만족하지 않는다고 결론지을 수 있다.
다음은 등분산을 검정하는 방법이다.
Levene's test를 사용하여 두 표본의 등분산성을 검정할 수 있다.
library(car)
levene_test_result <- leveneTest(converted ~ unit, data = df)
levene_test_result또는 F-test를 사용하여 두 표본의 등분산성을 검정할 수 있다.
f_test_result <- var.test(converted ~ unit, data = df)
f_test_resultLevene's test와 F-test의 p-value가 0.05보다 작아서 두 표본의 분산이 동일하다고 가정할 수 없다.
따라서 이 경우에는 표본이 정규성과 등분산성을 만족하지 않으므로, 비모수적 방법인 Wilcoxon Mann-Whitney rank sum test를 사용하는 것이 바람직하다. R에서는 wilcox.test를 사용하여 두 표본의 평균이 통계적으로 유의미하게 다른지 검정할 수 있다.
wilcox_test_result <- wilcox.test(
converted ~ unit,
data = df,
conf.int = TRUE
)
wilcox_test_result
Wilcoxon rank sum test with continuity correction
data: converted by unit
W = 1145, p-value = 0.02815
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-9.3599953 -0.8000423
sample estimates:
difference in location
-5.278598 30.3.1 만약 두 표본이 정규성을 만족했다면…
두 표본이 정규성을 만족했다면 다음 2가지 방법으로 독립 표본 t-test를 수행할 수 있다.
- 등분산을 가정하지 않는 경우: Welch’s t-test를 수행할 수 있다(
default). - 등분산을 가정하는 경우: 독립 표본 t-test를 수행할 수 있다(
var.equal = TRUE).
등분산을 가정하지 않는 경우 Welch’s t-test를 수행할 수 있다. R에서 t.test() 함수에 var.equal = FALSE (default)옵션을 사용하여 Welch’s t-test를 수행할 수 있다.
t_test_result_welch <- t.test(
converted ~ unit,
data = df,
var.equal = FALSE
)
t_test_result_welch
Welch Two Sample t-test
data: converted by unit
t = -2.3071, df = 58.788, p-value = 0.02459
alternative hypothesis: true difference in means between group feet and group metres is not equal to 0
95 percent confidence interval:
-16.54308 -1.17471
sample estimates:
mean in group feet mean in group metres
43.69565 52.55455 등분산을 가정할 수 있는 경우에는 독립 표본 t-test를 수행할 수 있다. R에서 t.test() 함수에 var.equal = TRUE 옵션을 사용하여 독립 표본 t-test를 수행할 수 있다.
t_test_result <- t.test(
converted ~ unit,
data = df,
var.equal = TRUE
)
t_test_result
Two Sample t-test
data: converted by unit
t = -2.6147, df = 111, p-value = 0.01017
alternative hypothesis: true difference in means between group feet and group metres is not equal to 0
95 percent confidence interval:
-15.572734 -2.145052
sample estimates:
mean in group feet mean in group metres
43.69565 52.55455
30.4 대응 표본 t-test(paired t-test) 예제: waves 데이터셋
HSAUR2 패키지의 waves 데이터셋을 사용하여 대응 표본 t-test를 수행한다. 이 데이터셋은 조력 발전 시뮬레이션 데이터라고 했는데, 각 행의 한 사람이라고 봐도 무방하다. 한 사람에 대해 두 가지 방법을 적용한 결과라 생각하면 된다.
method1 method2
1 2.23 1.82
2 2.55 2.42
3 7.99 8.26
4 4.09 3.46
5 9.62 9.77
6 1.59 1.40
7 8.98 8.88
8 0.82 0.87
9 10.83 11.20
10 1.54 1.33이 경우는 한 사람에 대해 두 가지 방법을 적용한 결과이므로, 대응 표본 t-test를 수행할 수 있다.
값의 차이를 구하자.
waves <- waves |>
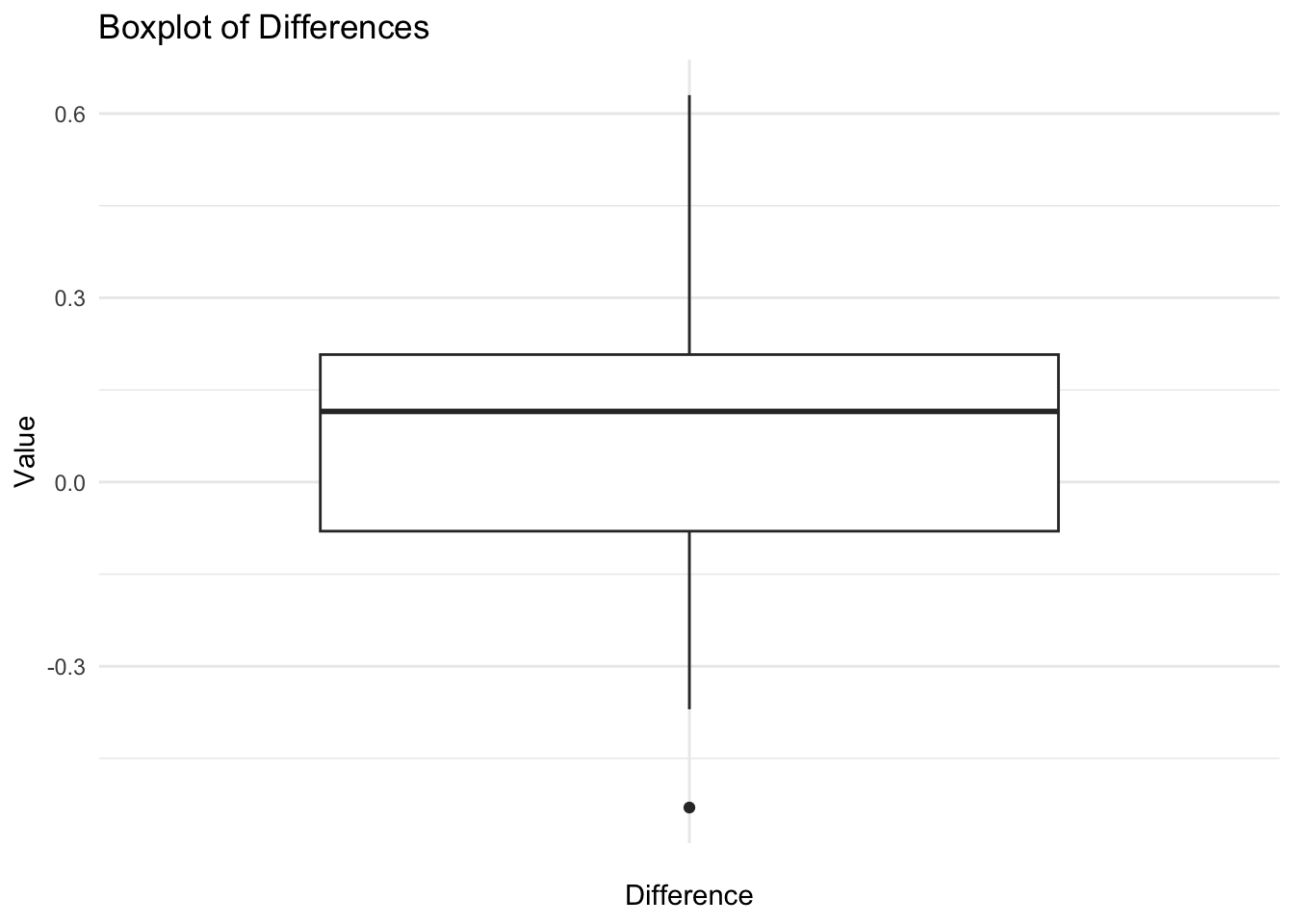
mutate(difference = method1 - method2)박스 플롯과 q-q plot을 사용하여 정규성을 확인할 수 있다.
waves |>
ggplot(aes(x = "", y = difference)) +
geom_boxplot() +
labs(
x = "Difference",
y = "Value",
title = "Boxplot of Differences"
) +
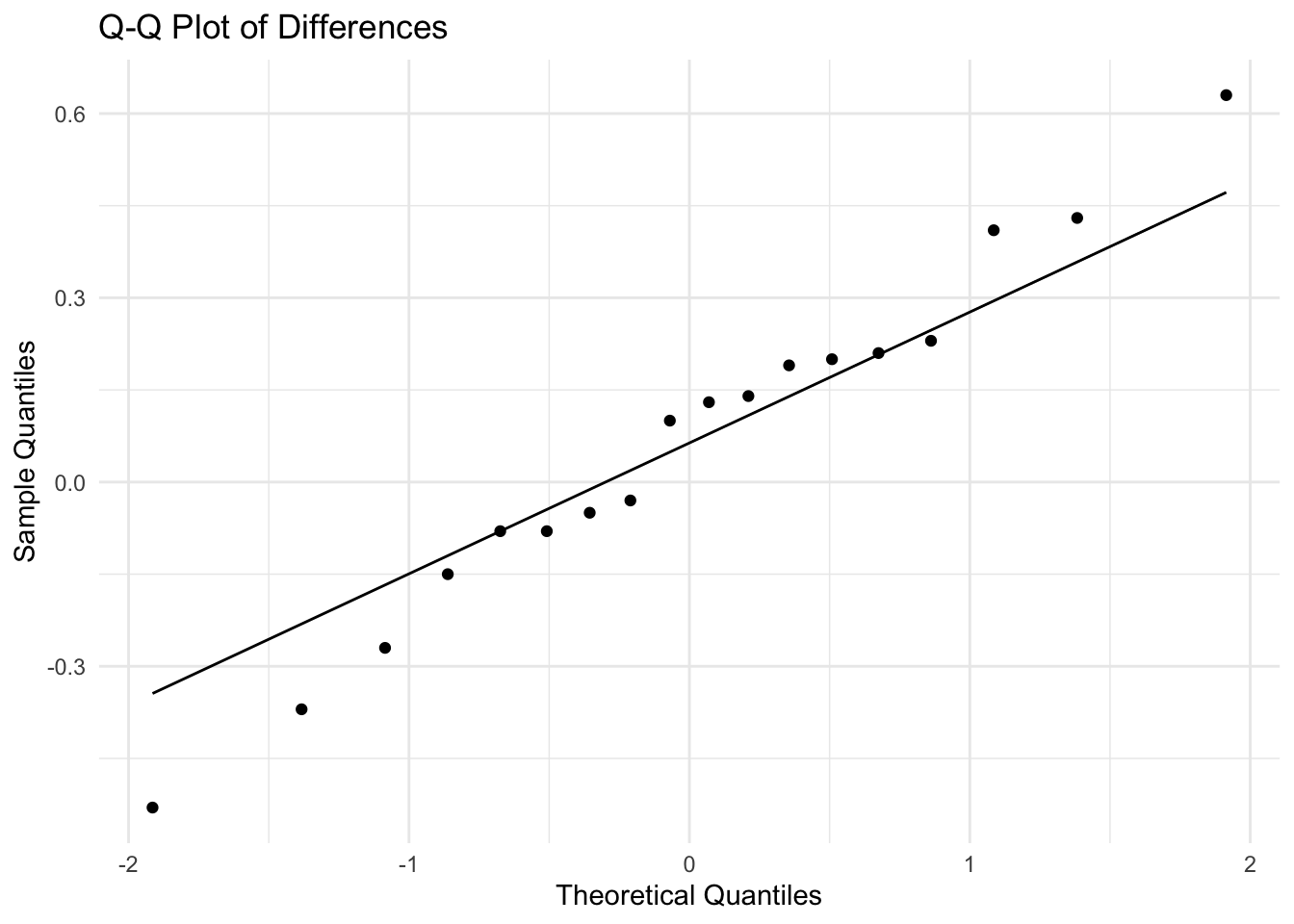
theme_minimal()waves |>
ggplot(aes(sample = difference)) +
stat_qq() +
stat_qq_line() +
labs(
title = "Q-Q Plot of Differences",
x = "Theoretical Quantiles",
y = "Sample Quantiles"
) +
theme_minimal()Shapiro-Wilk test를 사용하여 정규성을 검정할 수 있다.
shapiro_test_result <- shapiro.test(waves$difference)
shapiro_test_result
Shapiro-Wilk normality test
data: waves$difference
W = 0.98346, p-value = 0.9785Shapiro-Wilk test의 p-value가 0.05보다 크므로, 귀무가설을 기각하지 못하고, 데이터가 정규분포를 따른다고 결론지을 수 있다. 따라서 대응 표본 t-test를 수행할 수 있다. R에서 t.test() 함수를 사용하여 대응 표본 t-test를 수행할 수 있다.
t_test_result <- t.test(
waves$method1,
waves$method2,
paired = TRUE
)
t_test_result
Paired t-test
data: waves$method1 and waves$method2
t = 0.90193, df = 17, p-value = 0.3797
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.08258476 0.20591810
sample estimates:
mean difference
0.06166667 또는 다음과 같이 difference 변수를 사용하여 대응 표본 t-test를 수행할 수 있다.
t_test_result <- t.test(
waves$difference,
mu = 0, # 귀무가설에서 차이가 0이라고 가정
alternative = "two.sided" # 양측 검정
)
t_test_result
One Sample t-test
data: waves$difference
t = 0.90193, df = 17, p-value = 0.3797
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.08258476 0.20591810
sample estimates:
mean of x
0.06166667 30.4.1 만약 정규성을 만족하지 않는다면…
정규성을 만족하지 않는 경우, 비모수적 방법인 Wilcoxon signed-rank test를 사용할 수 있다. R에서 wilcox.test() 함수를 사용하여 대응 표본의 순위 합 검정을 수행할 수 있다.
wilcox_test_result <- wilcox.test(
waves$method1,
waves$method2,
paired = TRUE
)Warning in wilcox.test.default(waves$method1, waves$method2, paired = TRUE):
cannot compute exact p-value with tieswilcox_test_result
Wilcoxon signed rank test with continuity correction
data: waves$method1 and waves$method2
V = 109, p-value = 0.3165
alternative hypothesis: true location shift is not equal to 0또는 다음과 같이 difference 변수를 사용하여 대응 표본의 순위 합 검정을 수행할 수 있다.
wilcox_test_result <- wilcox.test(
waves$difference,
mu = 0, # 귀무가설에서 차이가 0이라고 가정
alternative = "two.sided" # 양측 검정
)Warning in wilcox.test.default(waves$difference, mu = 0, alternative =
"two.sided"): cannot compute exact p-value with tieswilcox_test_result
Wilcoxon signed rank test with continuity correction
data: waves$difference
V = 109, p-value = 0.3165
alternative hypothesis: true location is not equal to 0