30  두 연속 변수의 상관관계: correlation

library(tidyverse)

상관(Correlation)은 두 연속 변수 간의 선형 관계를 측정하는 방법이다. 상두 연속 변수의 상관관계는 보통 Pearson 상관계수(Pearson correlation coefficient)를 사용하여 측정하는데, 이는 두 변수 간의 선형 관계의 강도와 방향을 나타낸다. Pearson 상관계수는 -1에서 1 사이의 값을 가지며, 0은 두 변수 간에 선형 관계가 없음을 의미한다. 양의 값은 두 변수가 함께 증가함을 나타내고, 음의 값은 한 변수가 증가할 때 다른 변수가 감소함을 나타낸다.

보통 다음 수식에 의해서 계산된다: \[ r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} \tag{30.1}\]

위에서 \(x_i\)와 \(y_i\)는 각각 두 변수의 관측치, \(\bar{x}\)와 \(\bar{y}\)는 각각 두 변수의 평균이다.

이것은 두 변수의 공분산(covariance)을 각 변수의 표준편차의 곱으로 나눈, 정규화된 값을 나타낸다.

30.1 편차(deviation), 공분산(covariance), 상관계수(correlation)에 대한 이해

상관관계를 어떤 한 변수가 이렇게 바뀌는 데 다른 변수가 어떻게 바뀌는지를 나타내는 지표이다. 상관관계를 이해하기 위해서는 먼저 편차(deviation), 공분산(covariance), 그리고 상관계수(correlation)에 대해 알아야 한다.

편차는 각 관측치가 평균으로부터 얼마나 떨어져 있는지를 나타내는 값이다. 편차는 다음과 같이 계산된다: \[ d_i = x_i - \bar{x} \]

간단한 R 코드로 계산해 보자. 먼저, 두 변수 x와 y를 생성하고, 각각의 편차를 계산해 보자.

set.seed(42)
x <- sample(1:10, 10, replace = TRUE)
y <- x + round(rnorm(10, mean = 0, sd = 2), 0)

위 코드는 임의의 수를 만들기 위한 것으로 크게 관심을 가질 필요는 없다. 다음과 같은 두 변수 x와 y가 있다고 가정하자.

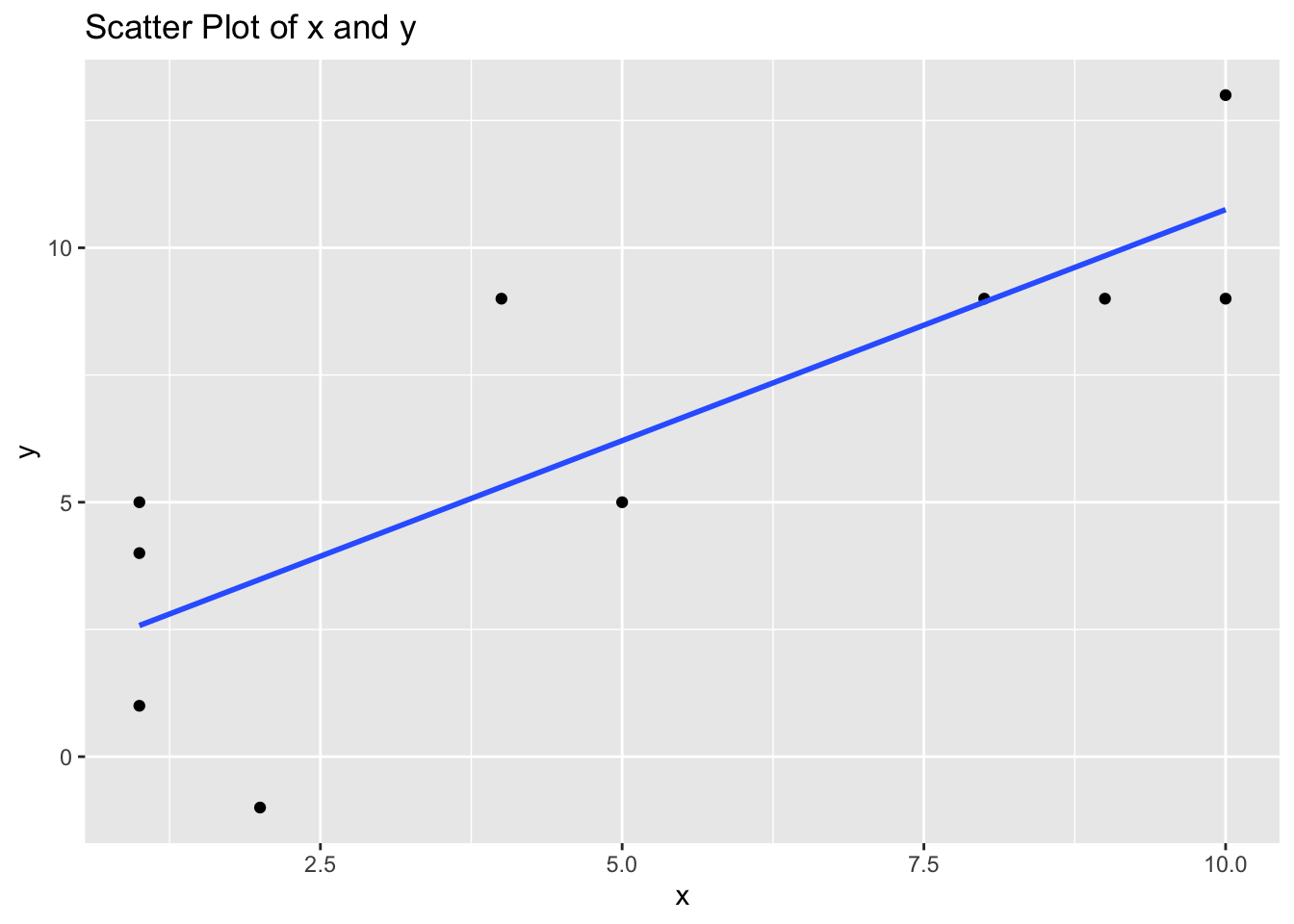
x

 [1]  1  5  1  9 10  4  2 10  1  8

y

 [1]  4  5  5  9 13  9 -1  9  1  9

두 연속 변수의 산점도를 그려보자.

dx <- data.frame(x)
dy <- data.frame(y)
df <- cbind(dx, dy)
df

    x  y
1   1  4
2   5  5
3   1  5
4   9  9
5  10 13
6   4  9
7   2 -1
8  10  9
9   1  1
10  8  9

df |>
    ggplot(aes(x = x, y = y)) +
    geom_point() +
    geom_smooth(method = "lm", se = FALSE) +
    labs(
        title = "Scatter Plot of x and y",
        x = "x",
        y = "y"
    )

`geom_smooth()` using formula = 'y ~ x'

편차(deviation)을 계산해 보자. 편차는 각 관측치가 평균으로부터 얼마나 떨어져 있는지를 나타낸다.

deviation_x <- x - mean(x)
deviation_y <- y - mean(y)

deviation_x

 [1] -4.1 -0.1 -4.1  3.9  4.9 -1.1 -3.1  4.9 -4.1  2.9

deviation_y

 [1] -2.3 -1.3 -1.3  2.7  6.7  2.7 -7.3  2.7 -5.3  2.7

공분산(covariance)은 두 변수 간의 편차의 곱의 평균이다.

covariance <- sum(deviation_x * deviation_y) / (length(x) - 1)
covariance

[1] 13.41111

cov() R 함수를 사용하여 계산할 수도 있다.

cov(x, y)

[1] 13.41111

즉 deviation_x와 deviation_y의 요소끼리 서로 곱한 후, 그 평균을 구한 것이다.

이런 공분산을 통해서 변수 x와 y가 얼마나 함께 변하는지를 알 수 있다. 공분산이 양수이면 두 변수가 함께 증가하거나 감소하는 경향이 있음을 나타내고, 음수이면 한 변수가 증가할 때 다른 변수가 감소하는 경향이 있음을 나타낸다.

즉, 공분산은 두 변수 간의 편차의 곱의 평균을 나타내며, 두 변수 간의 관계를 측정하는 데 사용된다. 공분산은 다음과 같이 계산된다: \[ cov(X, Y) = \frac{1}{n-1} \sum (x_i - \bar{x})(y_i - \bar{y}) \]

위 예에서 covariance는 12.0이었다. 이 값이 양수이기 때문에 x와 y가 함께 증가하는 것을 알았다. 그런데 공분산의 단점이 있다. 바로 공분산의 값이 두 변수의 측정 단위에 의존한다는 것이다. 즉, 두 변수의 단위가 다르면 공분산의 값도 달라진다. 예를 들어, x가 센티미터 단위이고, y가 미터 단위라면, 공분산의 값은 두 변수의 단위에 따라 달라질 것이다. 따라서, 공분산의 값을 해석하기가 어렵다. 그래서 공분산을 표준화한 상관계수(correlation coefficient)를 사용한다. 이 값을 -1에서1` 사이의 값으로 정규화하여, 두 변수 간의 관계를 더 쉽게 해석할 수 있다.

상관계수는 공분산을 각 변수의 표준편차의 곱으로 나눈 값이다. 상관계수는 다음과 같이 계산된다: \[ r = \frac{cov(X, Y)}{\sigma_X \sigma_Y} = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \sqrt{\sum (y_i - \bar{y})^2}} \]

R에서는 cor() 함수를 사용하여 상관계수를 계산할 수 있다. 먼저 위에서 계산한 covariance를 사용하여 상관계수를 계산해 보자.

correlation <- covariance / (sd(x) * sd(y))
correlation

[1] 0.8173169

cor(x, y)

[1] 0.8173169

30.2 두 연속 변수와의 상관관계 예제: water 데이터셋

이번에는 두 연속 변수 간의 상관관계를 살펴보자. HSAUR2 패키지의 water 데이터셋을 사용하여, 물의 경도(hardness)와 사망률(mortality) 간의 상관관계를 분석한다.

library(tidyverse)
library(HSAUR2)
data("water", package = "HSAUR2")
head(water)

  location       town mortality hardness
1    South       Bath      1247      105
2    North Birkenhead      1668       17
3    South Birmingham      1466        5
4    North  Blackburn      1800       14
5    North  Blackpool      1609       18
6    North     Bolton      1558       10

30.2.1 산점도와 회귀곡선

water |>
    ggplot(aes(x = hardness, y = mortality)) +
    geom_point() +
    geom_smooth(method = "lm", se = FALSE) +
    labs(
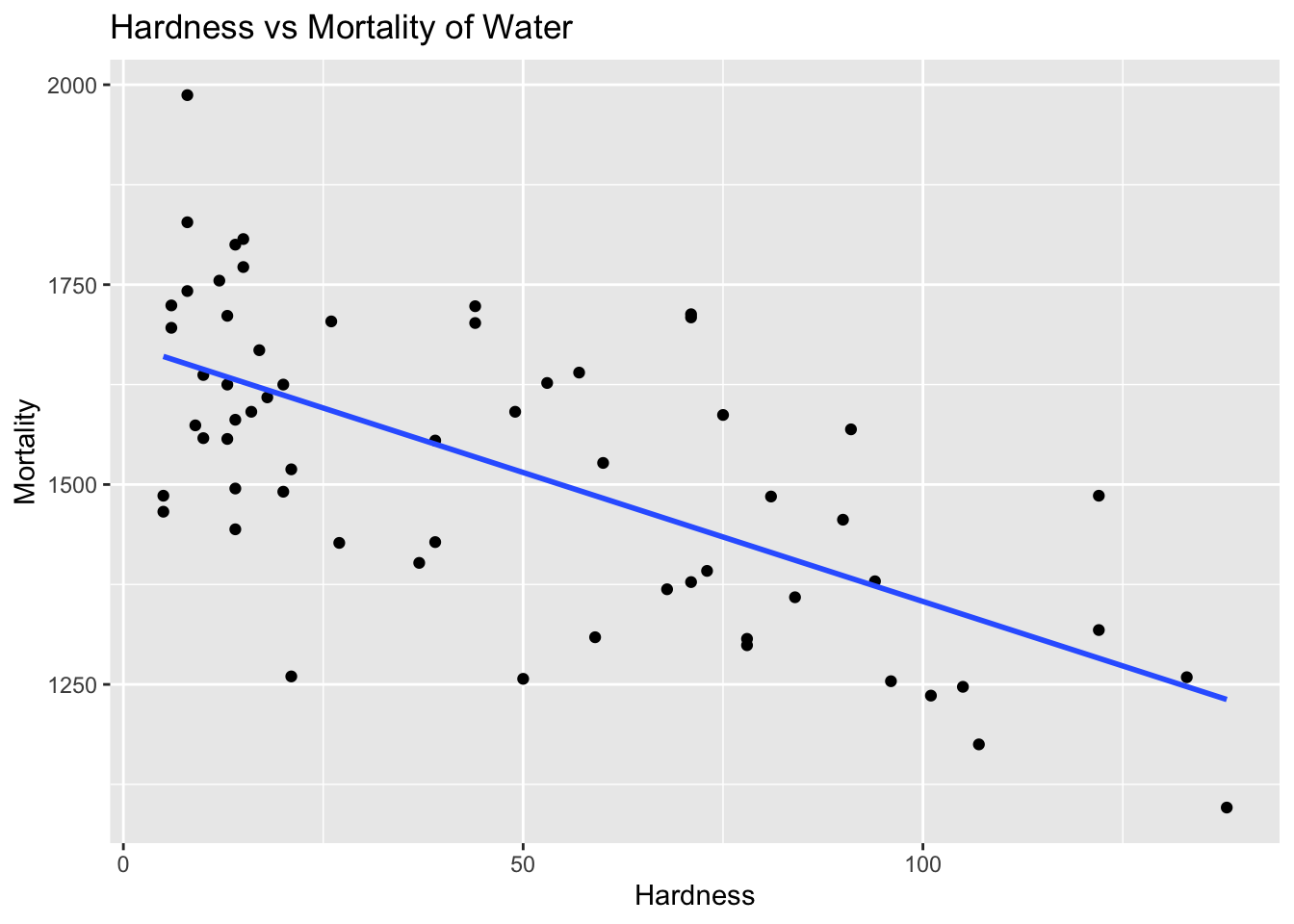
        title = "Hardness vs Mortality of Water",
        x = "Hardness",
        y = "Mortality"
    )

`geom_smooth()` using formula = 'y ~ x'

30.2.2 피어슨 상관계수

Hardness와 Mortality의 피어슨 상관계수를 계산해 보자.

cor(water$hardness, water$mortality)

[1] -0.6548486

30.3 상관관계에 대한 가설 검정

상관관계에 대한 가설 검정을 수행해 보자. 귀무가설은 두 변수 간에 상관관계가 없다는 것이다.

상관계수의 유의성을 검정하기 위해 cor.test() 함수를 사용할 수 있다.

사용되는 통계량은 다음과 같이 정의된다: \[ t = \frac{r \sqrt{n - 2}}{\sqrt{1 - r^2}} \]

여기서 \(r\)은 샘플 상관계수, \(n\)은 관측치의 수이다.

이 통계량은 상관계수가 0이고, bivatiate 정규분포를 따른다면, 이 통계량은 자유도 \(df = n - 2\)를 가지는 t-분포를 따른다.

cor.test(water$hardness, water$mortality)

    Pearson's product-moment correlation

data:  water$hardness and water$mortality
t = -6.6555, df = 59, p-value = 1.033e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.7783208 -0.4826129
sample estimates:
       cor 
-0.6548486 

30.4 두 연속 변수와의 순위 상관관계: 스피어만 상관계수

스피어만(Spearman) 상관계수는 두 변수 간의 순위(rank) 상관관계를 측정하는 방법이다. 이는 두 변수의 값이 아닌 순위를 기반으로 계산되며, 비모수적(non-parametric) 방법으로, 데이터가 정규분포를 따르지 않을 때 유용하다. 스피어만 상관계수는 다음과 같이 계산된다:

\[ \rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \]

위에서 \(d_i\)는 두 변수의 순위 차이, \(n\)은 관측치의 수이다.

매뉴얼로 위 x와 y의 스피어만 상관계수를 계산해 보자. 먼저 두 변수의 순위를 계산한다.

rank_x <- rank(x)
rank_y <- rank(y)

rank_x

 [1] 2.0 6.0 2.0 8.0 9.5 5.0 4.0 9.5 2.0 7.0

rank_y

 [1]  3.0  4.5  4.5  7.5 10.0  7.5  1.0  7.5  2.0  7.5

d <- rank_x - rank_y
d

 [1] -1.0  1.5 -2.5  0.5 -0.5 -2.5  3.0  2.0  0.0 -0.5

d_squared <- d^2
d_squared

 [1] 1.00 2.25 6.25 0.25 0.25 6.25 9.00 4.00 0.00 0.25

n <- length(x)
spearman_correlation <- 1 - (6 * sum(d_squared)) / (n * (n^2 - 1))
spearman_correlation

[1] 0.8212121

스피어만 상관계수는 cor() 함수의 method = "spearnman" 인자를 사용하여 게산할 수 있다.

cor(x, y, method = "spearman")

[1] 0.8122502

이 값에 대한 가설 검정을 수행할 수 있다. 귀무가설은 두 변수 간에 순위 상관관계가 없다는 것이다. cor.test() 함수의 method = "spearman" 인자를 사용하여 스피어만 상관계수에 대한 가설 검정을 수행할 수 있다.

cor.test(x, y, method = "spearman")

Warning in cor.test.default(x, y, method = "spearman"): Cannot compute exact
p-value with ties

    Spearman's rank correlation rho

data:  x and y
S = 30.979, p-value = 0.004305
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.8122502 

30.5 켄달의 타우(Kendall’s Tau)

켄달의 타우(Kendall’s Tau)는 두 변수 간의 순위 상관관계를 측정하는 또 다른 방법이다. 이 방법은 두 변수의 순위 간의 일치와 불일치를 기반으로 계산되는데 일치(concordant)와 불일치(discordant) 쌍의 수를 사용한다. 보통 일치되는 순위가 많은 경우 사용된다.

R에서 켄달의 타우를 계산하려면 cor() 함수의 method = "kendall" 인자를 사용한다. 먼저, 위에서 생성한 x와 y의 켄달의 타우를 계산해 보자.

cor(x, y, method = "kendall")

[1] 0.658703

30.6 infer 패키지를 사용한 상관관계 분석

library(infer)

obs_hat <- water |>
    specify(mortality ~ hardness) |>
    calculate(stat = "correlation")
obs_hat

Response: mortality (numeric)
Explanatory: hardness (numeric)
# A tibble: 1 × 1
    stat
   <dbl>
1 -0.655

null_dist <- water |>
    specify(mortality ~ hardness) |>
    hypothesize(null = "independence") |>
    generate(reps = 1000, type = "permute") |>
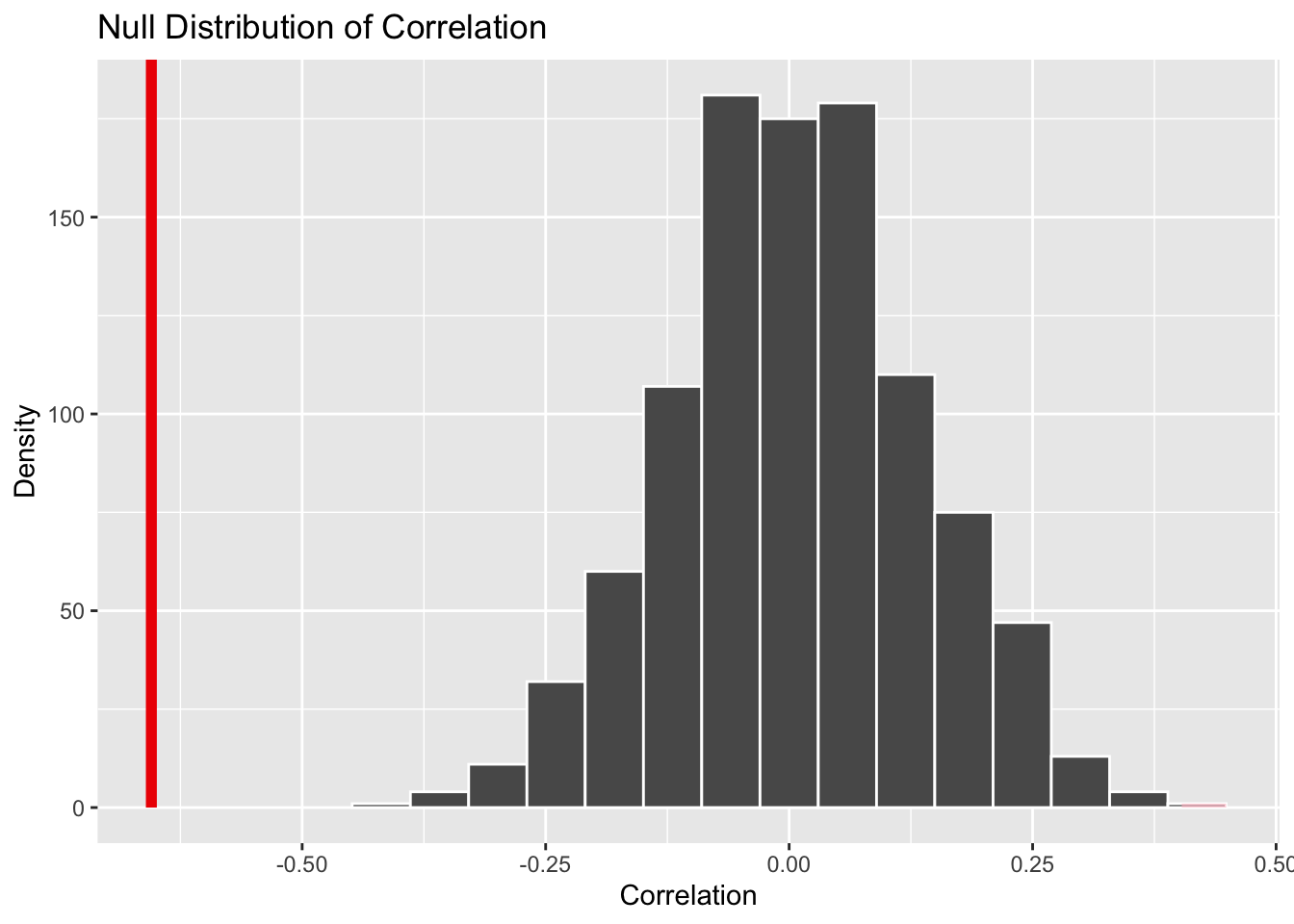
    calculate(stat = "correlation")

visualize(null_dist) +
    shade_p_value(obs_stat = obs_hat, direction = "two-sided") +
    labs(
        title = "Null Distribution of Correlation",
        x = "Correlation",
        y = "Density"
    )

null_dist |>
    get_p_value(obs_stat = obs_hat, direction = "two-sided")

Warning: Please be cautious in reporting a p-value of 0. This result is an approximation
based on the number of `reps` chosen in the `generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.

# A tibble: 1 × 1
  p_value
    <dbl>
1       0