40 로지스틱 회귀(Logistic Regression)과 일반화 선형 모델(Generalized Linear Model)
로지스틱 회귀(logistic regression)는 결과 변수(response variable)가 성공/실패, 질병 유무 등과 같이 범주형일 때 사용되는 통계 모델의 일종이다. 전형적인 선형 회귀는 결과 변수가 연속형일 때 사용하지만, 로지스틱 회귀는 결과 변수가 이진 분류(binary classification)일 때 사용된다.
R 언어를 사용하여 로지스틱 회귀를 수행할 때는 glm() 함수를 사용한다. GLM은 일반화 선형 모델(Generalized Linear Model)의 약자이다. 로지스틱 회귀가 일반화 선형 모델과 어떤 관계가 있길래 glm() 함수를 사용하여 로지스틱 회귀를 수행할 수 있는지 이해하기 위해서는 일반화 선형 모델의 개념을 개념적으로라도 이해할 필요가 있다.
40.1 로지스틱 회귀(Logistic Regression)
로지스틱 회귀는 결과 변수가 이진(yes or no, present or absent) 범주형일 때 사용되는 통계 모델이다. 이 모델은 선형 회귀와 유사하지만, 결과 변수를 확률로 변환하기 위해 로지스틱 함수를 사용한다.
이 말을 이해하기 위해서 기본 개념들을 살펴보자.
40.1.1 시그모이드 함수(Sigmoid Function)
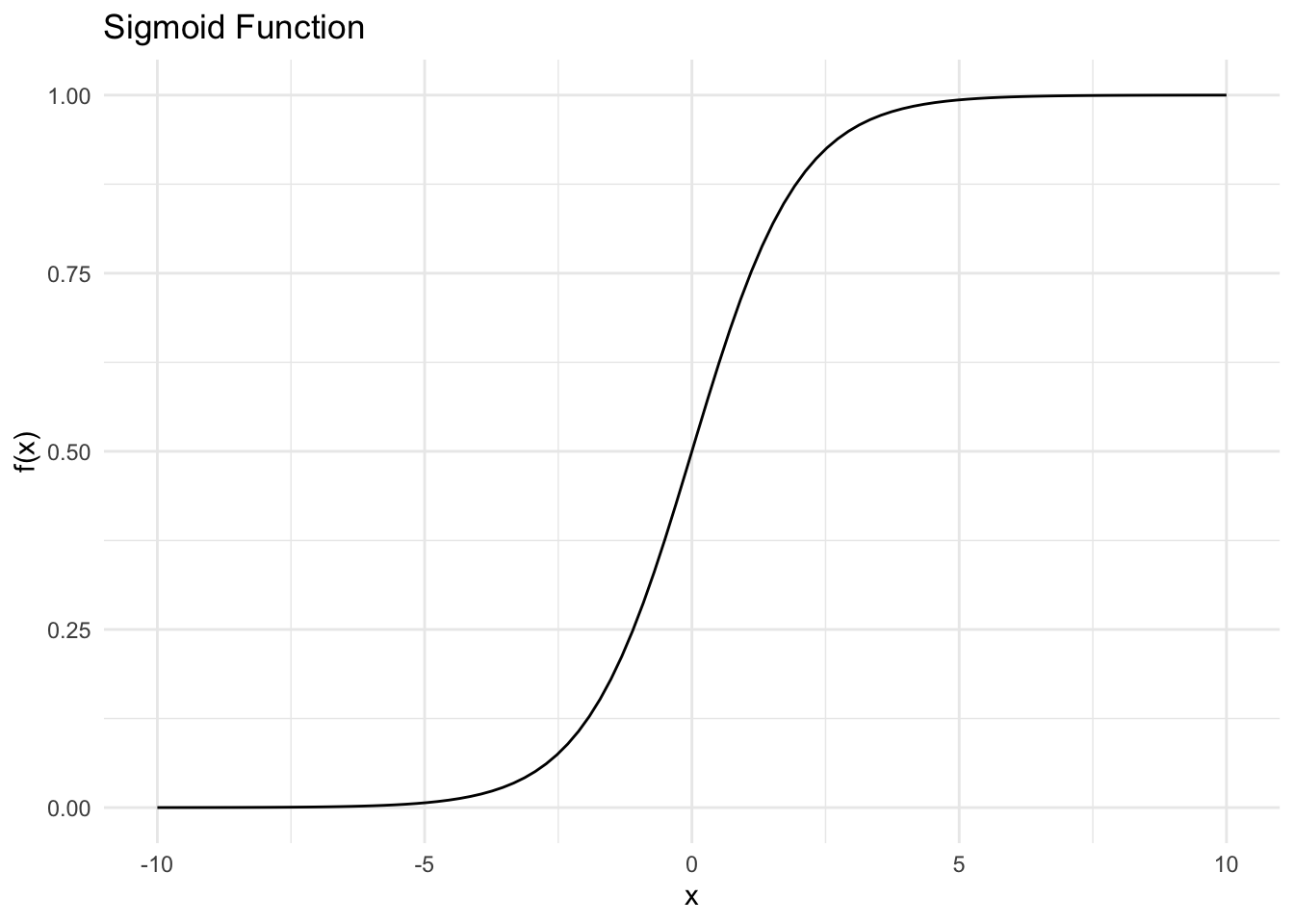
다음과 같은 함수르를 스그모이드 함수라고 부른다.
\[ f(x) = \frac{1}{1 + e^{-x}} \]
이 함수의 핵심적인 특징은 다음과 같다.
- 이 함수는 비선형 함수의 일종이다.
-
x의 값은 \(-\infty\)에서 \(\infty\)까지의 값을 가질 수 있다.y의 값은x가 \(-\infty\)에 가까워질수록 0에 가까워지고,x가 \(\infty\)에 가까워질수록 1에 가까워진다. 즉,y의 값은 항상 0과 1 사이에 있다. 우리가 로지스틱 회귀에서 이 함수를 사용하는 이유는 이렇게y의 값이 0과 1 사이에 있어서 확률로 해석할 수 있기 때문이다.
40.1.2 로지스틱 회귀의 모델
로지스틱 회귀는 위와 같은 시그모이드 함수를 사용하여 결과 변수를 확률로 변환한다. 로지스틱 회귀 모델은 다음과 같이 표현한다. 이 식을 통하면 설명 변수들이 어떠한 값을 만들더라도 그것을 0과 1 사이의 확률로 변환된다.
\[ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_i + \beta_2 x_2 + ... + \beta_k x_k)}} \tag{40.1}\]
왼쪽 항을 확률 p로 놓고, 오른쪽 항의 선형 조합을 \(\eta\)(“에타”라고 읽는다)로 놓으면 다음과 같이 쓸 수 있다.
\[ p = \frac{1}{1 + e^{-\eta}} \tag{40.2}\]
이때 \(\eta\)는 다음 부분을 말한다.
\[ \eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k \]
방정식 40.2를 \(\eta\)에 대해 정리하면 다음과 같이 된다.
\[ \eta = \log\left(\frac{p}{1-p}\right) \]
좌, 우항을 바꾸고 풀어 쓰면 다음과 같이 된다.
\[ \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k \tag{40.3}\]
이것을 로짓 함수(logit function)라고 한다. 로짓 함수는 확률을 로그-오즈(log-odds)로 변환하는 함수이다. 즉, 로지스틱 회귀는 결과 변수를 확률로 변환하고, 이 확률을 로그 오즈로 표현한다.
40.2 R 언어로 로지스틱 회귀 실행
다음과 같이 베이스 R 언어의 glm() 함수를 사용하여 로지스틱 회귀를 실행할 수 있다. glm은 일반화 선형 모델(Generalized Linear Model)의 약자이다. 로지스틱 회귀는 이 함수의 family 인자를 binomial(link = 'logit')로 설정하여 수행한다.
결과 해석은 뒤에서 자세히 다룰 예정이다.
library(palmerpenguins)
penguins <- na.omit(penguins)
# 펭귄 체중을 사용하여 성별을 예측하는 로지스틱 회귀 모델
m1 <- glm(sex ~ body_mass_g, family = binomial(link = "logit"), data = penguins)
summary(m1)
Call:
glm(formula = sex ~ body_mass_g, family = binomial(link = "logit"),
data = penguins)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -5.1625416 0.7243906 -7.127 1.03e-12 ***
body_mass_g 0.0012398 0.0001727 7.177 7.10e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 461.61 on 332 degrees of freedom
Residual deviance: 396.64 on 331 degrees of freedom
AIC: 400.64
Number of Fisher Scoring iterations: 4이런 결과에 사용되는 용어들은 일반화 선형 모델과 관련이 있다.
40.3 일반화 선형 모델(Generalized Linear Model, GLM)
일반화 선형 모델이 통계학사에서 차지하는 의의를 살펴보자. 다음은 ChatGPT가 정리한 내용이다. 일반화 선형 모델에 관해 비교적 잘 정리된 자료가 있으니 여기를 참고하자.
-
GLM의 등장: 통계학의 통합적 혁신
- John Nelder와 Robert Wedderburn (1972)이 GLM 체계를 정립.
- 등장 전:
- 선형 회귀: 연속형 변수, 정규분포
- 로지스틱 회귀: 이항형 변수
- 포아송 회귀: 카운트형 변수
각 모델이 별도의 이론과 방법론으로 분리되어 있던 것을, GLM이 통합적인 수학적 틀로 묶음.
- GLM의 구조:
- 지수분포족 기반 확률모형
- 링크 함수와 선형 예측자의 조합
- 일관된 추정, 해석, 평가 방법론 제공
-
통계학사에서 GLM의 위치
시대 통계학 발전 19세기 최소제곱법, 선형 회귀 (Gauss, Legendre) 20세기 초 이항, 포아송, 프로빗/로짓 모델 개발 1970s GLM의 공식화 (Nelder & Wedderburn, 1972) 이후 GLM 기반 확장: GAM, GLMM, GEE, Bayesian GLM 등 - GLM은 고전통계와 현대통계의 연결고리로서 중요한 위치를 차지.
-
GLM의 학문적 의의
- 이론적 통합성: 다양한 자료 형태를 하나의 수학적 언어로 표현
- 해석 가능성: 계수의 통계적 해석이 일관
- 추정의 표준화: 최대우도법(MLE) 기반의 표준화된 추정
- 응용 확장: 공공보건, 생물통계, 사회과학, 금융 등에서 폭넓게 활용
-
이후 영향
- GLM 이후 등장한 주요 모델 및 방법론:
- GAM (Generalized Additive Models): 비선형 함수의 유연한 확장
- GLMM (Generalized Linear Mixed Models): 랜덤 효과 포함
- Bayesian GLM: 베이지안적 접근 확장
- 머신러닝: 로지스틱 회귀, softmax regression 등 기법의 수학적 기반
- GLM 이후 등장한 주요 모델 및 방법론:
-
결론
GLM은 “현대 통계학의 중추적인 혁신”으로, 데이터를 보는 방식과 모델링하는 방식을 근본적으로 확장한 개념.
-
참고
- Nelder, J.A. and Wedderburn, R.W.M. (1972). “Generalized Linear Models”. Journal of the Royal Statistical Society, Series A.
- 현대 통계학 및 머신러닝 교재들에서 GLM은 핵심적 이론적 기반으로 다룸.
40.3.1 통계학에서의 선형(linear) vs 비선형(non-linear)
통계학에서 선형성(linearity)는 모델의 결과 변수와 파라미터(계수) 사이의 관계가 선형적(linear)이라는 것을 의미한다. 따라서, 다음과 같은 모델들은 선형 모델이다.
\[ \begin{align*} y &= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k \\ y &= \beta_0 + \beta_1 x + \beta_2 x^2 \end{align*} \]
반면 통계학에서 비선형 모델(non-linear model)은 결과 변수와 파라미터 사이의 관계가 선형적이지 않은 모델을 의미한다. 다음은 비선형 모델이다.
\[ \begin{align*} y = \beta_0 e^{\beta_1 x} \end{align*} \]
위에서 로지스틱 회귀 모델은 다음과 같이 표현된다. 로지스틱 회귀 모델은 비선형 모델의 일종이다.
\[ p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_i + \beta_2 x_2 + ... + \beta_k x_k)}} \tag{40.4}\]
로지스틱 회귀가 목표하는 것은 결과 변수의 클래스(class)이다. 클래스는 범주형 변수로, 예를 들어 성공/실패, 질병 유무 등이다. 즉, 이런 결과들 사이에는 본질적으로 선형 관계가 존재하지 않는다.
위 식을 로짓함수를 사용하여 바꾸면 다음과 같이 된다. 즉, 비선형적인 관계를 선형적으로 바꾼다.
\[ \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k \tag{40.5}\]
이와 같이 일반화 선형 모델은 결과 변수와 파라미터 사이의 관계가 선형적이지 않은 모델을 선형적으로 바꾸어 분석할 수 있도록 해 준다.
40.3.2 선형 모델의 확장
GLM은 선형 회귀 모델의 확장하여, 다양한 종류의 결과 변수에 대해 적용할 수 통합적인 프레임워크이다. GLM은 다음과 같은 세 가지 주요 구성 요소로 구성된다.
-
선형 예측기(Linear Predictor): 결과 변수와 설명 변수 간의 선형 관계를 나타내는 부분이다. 이는 다음과 같이 표현된다. \[ \eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k \]
여기서 \(\eta\)는 선형 예측기, \(\beta_0\)는 절편(intercept), \(\beta_1, \beta_2, ..., \beta_k\)는 설명 변수의 계수(coefficient), \(x_1, x_2, ..., x_k\)는 설명 변수이다.
링크 함수(Link Function): 결과 변수와 선형 예측기 간의 관계를 정의하는 함수이다. GLM은 다양한 종류의 링크 함수를 지원하며, 이는 결과 변수의 분포에 따라 다르게 설정된다. 예를 들어, 로지스틱 회귀에서는 로짓(link = ‘logit’) 함수를 사용한다. 참고로 선형과 비선형을 연결한다는 의미로 링크 함수라고 부른다. 로지스틱 회귀에서는 다음과 같이 표현된다. \[ g(\mu) = \eta \] 여기서 \(g\)는 링크 함수, \(\mu\)는 결과 변수의 기대값(평균)이다.
분포(Distribution): 결과 변수의 분포를 정의한다. GLM은 다양한 종류의 분포를 지원하며, 이는 결과 변수의 특성에 따라 다르게 설정된다. 예를 들어, 로지스틱 회귀에서는 이항 분포(binomial distribution)를 사용한다.
40.3.3 최대 우도 추정(Maximum Likelihood Estimation, MLE)
GLM에서 회귀 모델의 매개변수 \(\beta_0, \beta_1, \beta_2, ..., \beta_k\)를 추정하기 위해서는 최대 우도 추정(Maximum Likelihood Estimation, MLE)을 사용한다. MLE는 주어진 데이터에 대해 가능한 매개변수를 찾는 방법이다. 즉, 주어진 데이터가 가장 잘 설명되는(Likelihood가 최대가 되는) 매개변수를 찾는다.
MLE는 다음과 같은 과정을 거친다.
- 가능도 함수(Likelihood Function): 주어진 데이터에 대해 가능한 매개변수의 조합을 계산한다. 이때, 각 관측치가 주어진 매개변수 하에서 발생할 확률을 곱하여 가능도 함수를 정의한다. 식으로 표현하면 다음과 같다. \[ L(\beta) = \prod_{i=1}^{n} p_i^{y_i} (1 - p_i)^{1 - y_i} \]
여기서 \(p_i\)는 관측치 \(i\)의 예측된 확률, \(y_i\)는 관측치의 실제 값이다. 이 식은 각 관측치가 주어진 매개변수 하에서 발생할 확률을 곱한 것이다.
\(\prod_{i=1}^{n}\)은 곱셈을 나타내는 기호이다. “파이”라고 읽는다. \(i\)가 1부터 \(n\)까지의 값을 가지는 모든 항을 곱한다는 의미이다.
\[ \prod_{i=1}^{n} x_i = x_1 \cdot x_2 \cdot ... \cdot x_n \]
로그 가능도 함수(Log-Likelihood Function): 가능도 함수는 곱셈 형태이므로, 계산을 용이하게 하기 위해 로그를 취하여 로그 가능도 함수를 정의한다. 로그 가능도 함수는 다음과 같이 표현된다. \[ \log L(\beta) = \sum_{i=1}^{n} \left[ y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right] \] 여기서 \(y_i\)는 관측치의 실제 값, \(p_i\)는 예측된 확률이다.
최적화(Optimization): 로그 가능도 함수를 최대화(또는 그 음수를 최소화하는)하는 매개변수 \(\beta\)를 찾는다. 이는 수치 최적화 기법을 사용하여 수행된다.
추정된 매개변수: 최적화 결과로 얻어진 매개변수 \(\beta\)는 로지스틱 회귀 모델의 추정된 매개변수이다.
40.3.3.1 구체적인 값으로 가능도를 계산해 보기 (with ChatGPT)
가능도라는 용어가 추상적이어서 좀 더 구체적인 예를 살펴보려고 한다. 주사위를 5번 던져서 3이 나오는 경우에 대한 확률과 likelihood, log-likelihood를 계산해보자.
가능도라는 것은 주어진 모델하에서 얻어진 데이터를 관측할 확률을 의미한다. 여기서 주어진 모델은 주사위를 던져서 3이 나오는 경우에 대한 모델이다.
- 주사위를 1번 던져서 3이 나올 확률은 \(p = \frac{1}{6}\)이다.
- 주사위를 1번 던져서 3이 나오지 않을 확률은 \(1 - p = \frac{5}{6}\)이다.
이러한 모델하에서 다음 확률을 계산한다.
- 주사위를 5번 던졌을 때 y = [1, 0, 0, 1, 0]과 같은 결과를 얻었다고 가정해 보자.
1은 3이 나온 경우,0은 3이 나오지 않은 경우이다.
이때, likelihood는 다음과 같이 계산된다.
\[ L(\beta) = p^2 \cdot (1 - p)^3 = \left(\frac{1}{6}\right)^2 \cdot \left(\frac{5}{6}\right)^3 \]
보통 수식을 일반화하여 계산하는 경우가 많은데, 이렇게 곱으로 표현한 것에 로그를 취하면 곱이 합으로 바뀌므로 계산이 용이해진다. 그렇게 한 것이 로그 가능도(log-likelihood)이다.
\[ \log L(\beta) = 2 \log\left(\frac{1}{6}\right) + 3 \log\left(\frac{5}{6}\right) \]
만약 주사위를 n번 던졌을 때, 3이 나온 횟수를 \(k\)라고 하면, 위 식은 다음과 같이 일반화된다.
\[ \log L(\beta) = k \log\left(\frac{1}{6}\right) + (n - k) \log\left(\frac{5}{6}\right) \]
확률을 p로 놓으면, 위 식은 다음과 같이 쓸 수 있다.
\[ \log L(\beta) = k \log(p) + (n - k) \log(1 - p) \]
40.4 R 로지스틱 회귀(일반화 선형 모델) 실행
로지스틱 회귀는 일반화 선형 모델의 일종이다. 일반화 선형 모델의 용어로 해석하면 다음과 같다.
- 선형 예측기(Linear Predictor):
- \(\eta = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k\)
- 링크 함수(Link Function):
- 로짓 함수: \(g(\mu) = \log\left(\frac{\mu}{1 - \mu}\right)\)
- 분포(Distribution):
- 이항 분포: \(Y \sim \text{Binomial}(n, p)\)
그래서 R glm() 함수에서 로지스틱 회귀를 할 때 다음과 같이 사용한다.
glm(sex ~ body_mass_g, family = binomial(link = "logit"), data = penguins)실제 palmerpenguins 데이터셋을 사용하여 로지스틱 회귀를 실행해 보자. 이 데이터셋은 펭귄의 다양한 특성(예: 체중, 길이 등)과 성별 정보를 포함하고 있다. 여기서는 펭귄의 체중(body_mass_g)을 사용하여 성별(sex)을 예측하는 로지스틱 회귀 모델을 만들어 보자.
library(palmerpenguins)
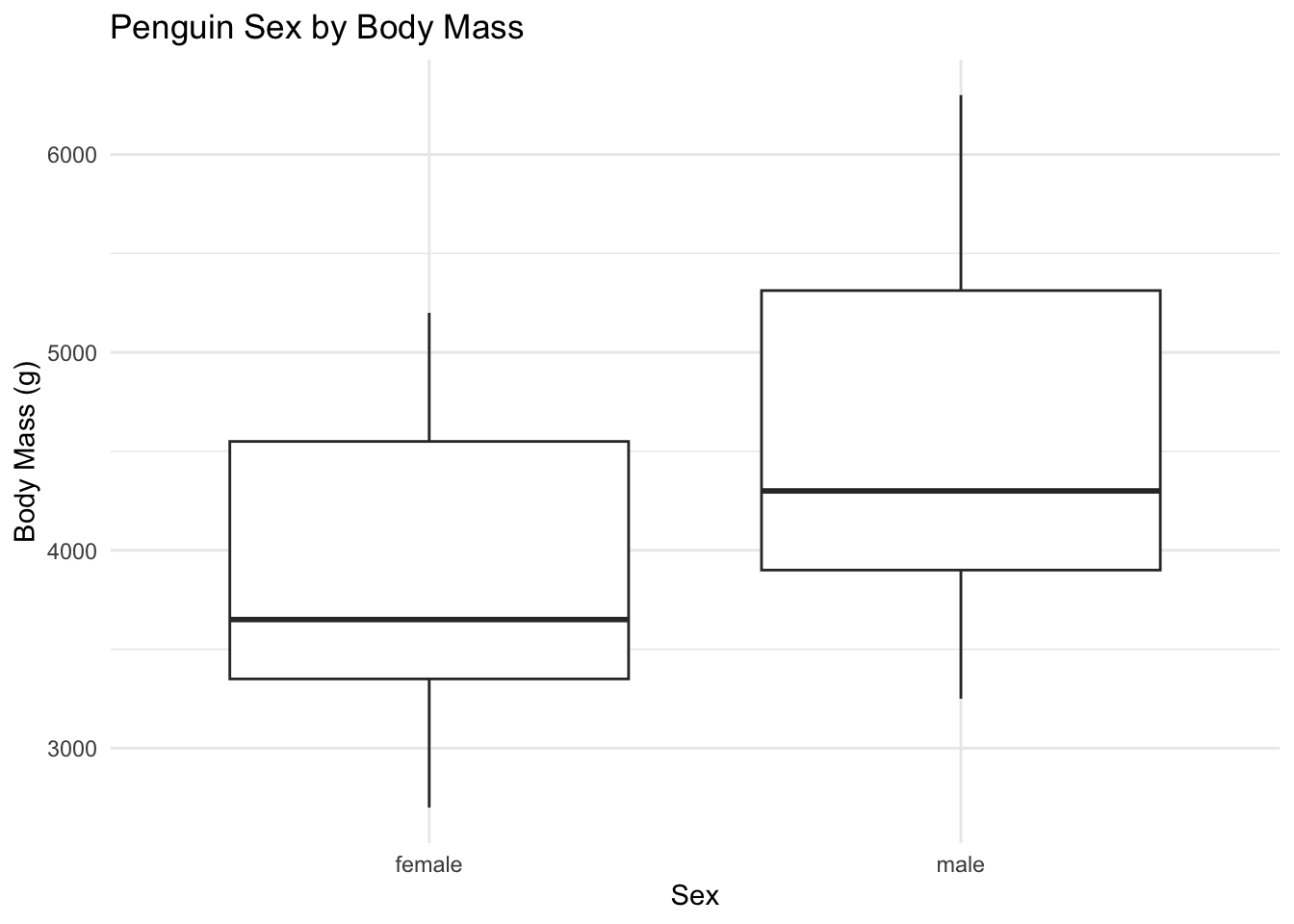
penguins <- na.omit(penguins) # 결측치 제거먼저 성별(sex)과 체중(body_mass_g) 간의 관계를 박스 플롯으로 시각화해 보자. 이 그래프는 성별에 따른 체중의 분포를 보여준다.
library(ggplot2)
ggplot(penguins, aes(x = sex, y = body_mass_g)) +
geom_boxplot() +
labs(title = "Penguin Sex by Body Mass", x = "Sex", y = "Body Mass (g)") +
theme_minimal()다음은 glm() 함수를 사용하여 로지스틱 회귀 모델을 실행하는 코드이다. 이 모델은 펭귄의 체중을 사용하여 성별을 예측한다.
R glm() 함수를 사용할 때, 결과 변수의 카테고리 순서가 중요하다. 예를 들어, sex 변수가 male과 female 두 가지 카테고리를 가지고 있다면, 이 순서가 모델의 결과에 영향을 미친다. 이것을 결정하는 것은 결과 변수(factor)의 레벨(level) 순서이다. 이를테면 이 경우 leves() 함수를 사용하여 sex 변수의 레벨 순서를 확인할 수 있다.
levels(penguins$sex)[1] "female" "male" 이 결과는 female, male 순으로 되어 있다. 그래서 이진 분류인 경우에는 female이 0으로 male이 1로 해석된다. 따라서 아래 로지스틱 회귀는 male일 확률을 예측하는 모델이 된다.
# 펭귄 체중을 사용하여 성별을 예측하는 로지스틱 회귀 모델
m1 <- glm(sex ~ body_mass_g, family = binomial(link = "logit"), data = penguins)
summary(m1)
Call:
glm(formula = sex ~ body_mass_g, family = binomial(link = "logit"),
data = penguins)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -5.1625416 0.7243906 -7.127 1.03e-12 ***
body_mass_g 0.0012398 0.0001727 7.177 7.10e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 461.61 on 332 degrees of freedom
Residual deviance: 396.64 on 331 degrees of freedom
AIC: 400.64
Number of Fisher Scoring iterations: 4m1$coefficients (Intercept) body_mass_g
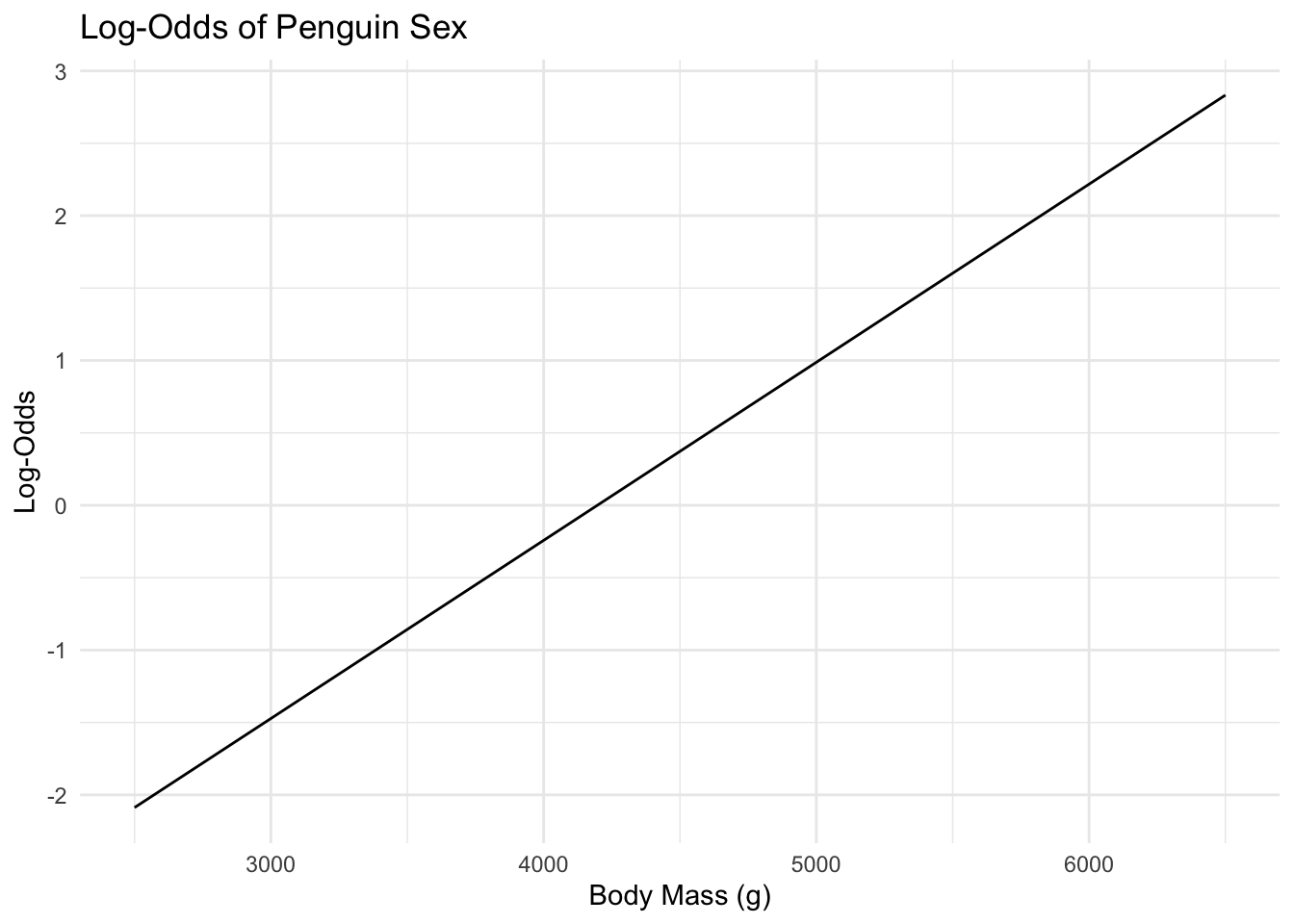
-5.162541644 0.001239819 이 결과를 보면 body_mass_g의 계수는 약 0.00123이고, 절편(intercept)은 약 -5.1625이다. log-odds 직선의 기울이가 약 0.00123이라는 것은 body_mass_g가 1 gram 증가할 때마다 log-odds의 값이 약 0.00123만큼 증가한다는 것을 의미한다. 그래프로 나타내면 다음과 같다.
library(ggplot2)
x <- seq(2500, 6500, length.out = 100)
beta_0 <- -5.1625
beta_1 <- 0.00123
log_odds <- beta_0 + beta_1 * x
data <- data.frame(body_mass_g = x, log_odds = log_odds)
ggplot(data, aes(x = body_mass_g, y = log_odds)) +
geom_line() +
labs(title = "Log-Odds of Penguin Sex", x = "Body Mass (g)", y = "Log-Odds") +
theme_minimal()이 결과를 원래의 데이터 값을 가지고 다시 해석하기 위해서는 log-odds를 확률로 변환해 볼 필요가 있다.
로지스틱 회귀에서 예측 확률은 다음과 같이 계산된다. \[ p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x)}} \]
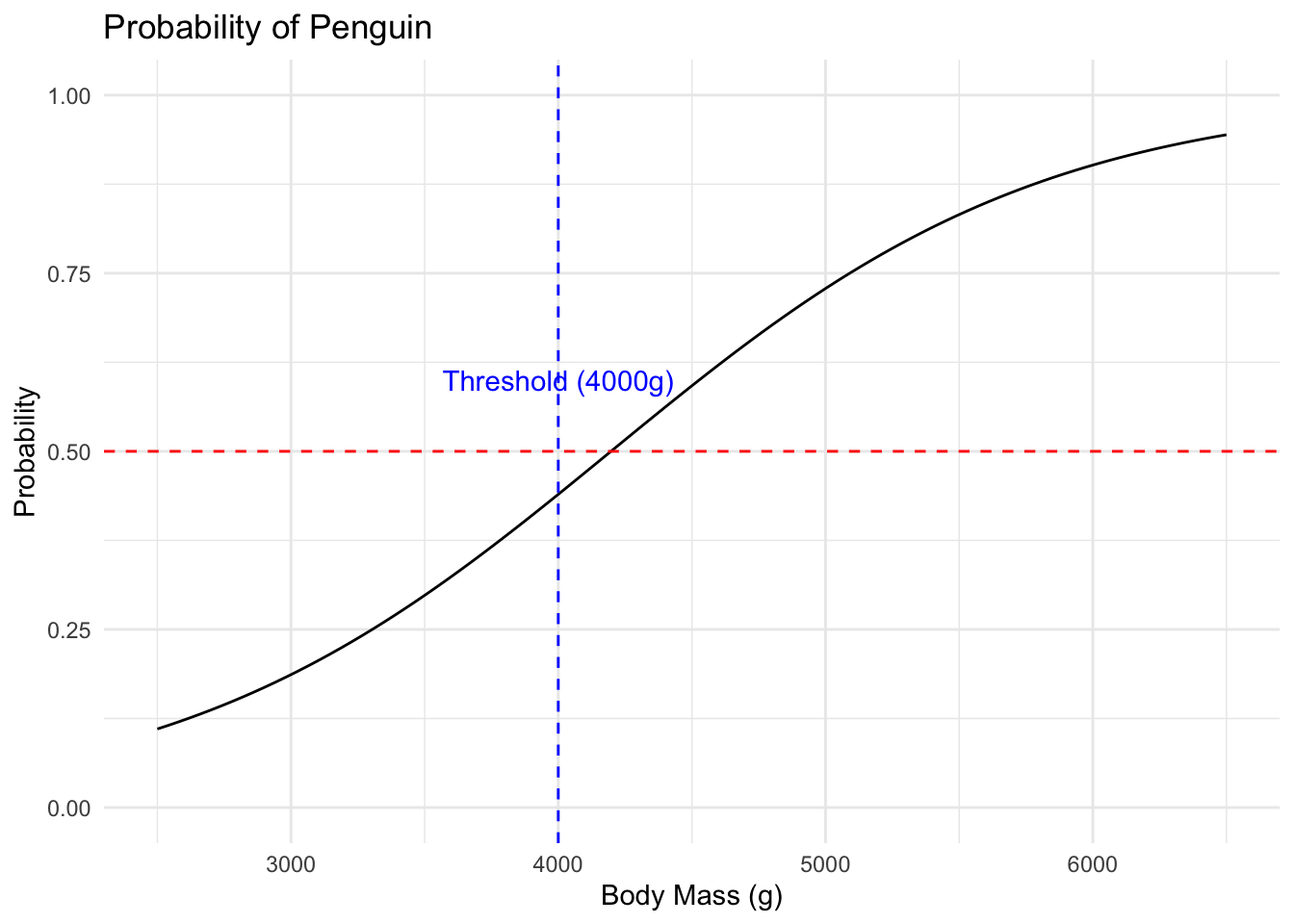
이 식을 가지고 확률에 대한 그래프를 그려보면 다음과 같다.
library(ggplot2)
penguins <- na.omit(penguins)
x <- seq(2500, 6500, length.out = 100)
beta_0 <- -5.1625
beta_1 <- 0.00123
p <- 1 / (1 + exp(-(beta_0 + beta_1 * x)))
data <- data.frame(body_mass_g = x, probability = p)
ggplot(data, aes(x = body_mass_g, y = probability)) +
geom_line() +
labs(title = "Probability of Penguin", x = "Body Mass (g)", y = "Probability") +
theme_minimal() +
ylim(0, 1) +
geom_hline(yintercept = 0.5, linetype = "dashed", color = "red") +
geom_vline(xintercept = 4000, linetype = "dashed", color = "blue") +
annotate("text", x = 4000, y = 0.6, label = "Threshold (4000g)", color = "blue")체중이 3000 gram인 경우이다.
# 체중이 3000g인 경우의 log-odds와 확률 계산
body_mass_g <- 3000
log_odds <- beta_0 + beta_1 * body_mass_g
probability <- 1 / (1 + exp(-log_odds))
log_odds[1] -1.4725probability[1] 0.1865629다음은 체중이 4000 gram인 경우이다.
# 체중이 4000g인 경우의 log-odds와 확률 계산
body_mass_g <- 4000
log_odds <- beta_0 + beta_1 * body_mass_g
probability <- 1 / (1 + exp(-log_odds))
log_odds[1] -0.2425probability[1] 0.4396704다음은 체중이 5000 gram인 경우를 경우이다.
# 체중이 5000g인 경우의 log-odds와 확률 계산
body_mass_g <- 5000
log_odds <- beta_0 + beta_1 * body_mass_g
probability <- 1 / (1 + exp(-log_odds))
log_odds[1] 0.9875probability[1] 0.728593840.5 GLM의 Deviance
GLM의 deviance는 모델의 적합도를 평가하는 지표로 사용된다. deviance는 모델이 얼마나 잘 데이터를 설명하는지를 나타내며, 낮을수록 모델이 데이터를 잘 설명한다는 것을 의미한다. deviance는 다음과 같이 정의된다.
\[ D = -2 \log\left(\frac{L(\hat{\beta})}{L(\beta_0)}\right) \]
여기서 \(\hat{\beta}\)는 모델의 추정된 매개변수, \(L(\hat{\beta})\)는 추정된 매개변수 하에서의 가능도 함수, \(L(\beta_0)\)는 절편만 있는 모델의 가능도 함수이다. deviance는 모델의 적합도를 평가하는 데 사용되며, deviance가 낮을수록 모델이 데이터를 잘 설명한다는 것을 의미한다.
위 펭귄의 sex를 예측하는 로지스틱 회귀 모델의 deviance를 계산해 보자.
# deviance 계산
n <- nrow(penguins)
k <- length(m1$coefficients)
beta_0 <- m1$coefficients[1]
beta_1 <- m1$coefficients[2]
p <- 1 / (1 + exp(-(beta_0 + beta_1 * penguins$body_mass_g)))
deviance <- -2 * sum(log(ifelse(penguins$sex == "male", p, 1 - p)))
deviance[1] 396.6446이 deviance 값은 모델이 데이터를 얼마나 잘 설명하는지를 나타낸다. deviance가 낮을수록 모델이 데이터를 잘 설명한다는 것을 의미한다. 따라서 이 지표를 가지고 더 나은 모델을 찾거나, 모델의 적합도를 평가할 수 있다.
40.6 z-통계량(Wald Statistic): 각 계수의 유의성 평가
다음과 같은 결과에서 z value가 있는데, 이것은 각 계수의 유의성을 평가하는 데 사용되는 통계량이다. z value는 각 계수가 0이라는 귀무가설 하에서 얼마나 멀리 떨어져 있는지를 나타내는 지표이다.
Call:
glm(formula = sex ~ body_mass_g, family = binomial(link = "logit"),
data = penguins)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -5.1625416 0.7243906 -7.127 1.03e-12 ***
body_mass_g 0.0012398 0.0001727 7.177 7.10e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 461.61 on 332 degrees of freedom
Residual deviance: 396.64 on 331 degrees of freedom
AIC: 400.64
Number of Fisher Scoring iterations: 4GLM에서 계수의 유의성을 평가하기 위해 z-통계량(Wald Statistic)을 사용한다. z-통계량은 각 계수가 0이라는 귀무가설 하에서 얼마나 멀리 떨어져 있는지를 나타내는 지표이다. z-통계량은 다음과 같이 계산된다.
\[ z = \frac{\hat{\beta}_j}{SE(\hat{\beta}_j)} \]
여기서 \(\hat{\beta}_j\)는 계수의 추정값, \(SE(\hat{\beta}_j)\)는 계수의 표준 오차(standard error)이다. z-통계량은 정규 분포를 따르며, 이를 통해 각 계수의 유의성을 평가할 수 있다.
표준 오차를 계산하는 방법은 GLM 프레임워크에서 잘 정의되어 있다. 우리는 summary() 함수를 사용하여 GLM 모델의 계수와 표준 오차를 확인할 수 있다. 물론 summary() 함수에 z-통계량도 포함되어 있다.
# z-통계량 계산
z_statistic <- m1$coefficients / summary(m1)$coefficients[, "Std. Error"]
z_statistic(Intercept) body_mass_g
-7.126738 7.177459 이 z-통계량은 표준 정규 분포를 따르므로, 이를 통해 각 계수의 유의성을 평가할 수 있다. 일반적으로 z-통계량이 1.96보다 크면(또는 -1.96보다 작으면) 5% 유의 수준에서 해당 계수가 통계적으로 유의하다고 판단한다.
40.7 아카이케 정보 기준 (AIC,Akaike Information Criterion)
AIC(Akaike Information Criterion)는 모델의 적합도를 평가하는 데 사용되는 지표로, 모델의 복잡성과 적합도를 동시에 고려한다. AIC는 다음과 같이 정의된다.
\[ \text{AIC} = -2 \log(L) + 2k \]
여기서 \(L\)은 모델의 가능도 함수, \(k\)는 모델의 매개변수 개수이다.
이 경우 AIC를 직접 계산하면 다음과 같다.
# AIC 계산
p <- 1 / (1 + exp(-(beta_0 + beta_1 * penguins$body_mass_g)))
log_likelihood <- sum(log(ifelse(penguins$sex == "male", p, 1 - p)))
k <- length(m1$coefficients)
aic_value <- -2 * log_likelihood + 2 * k
aic_value[1] 400.6446다음과 같은 함수도 있다.
AIC(m1)[1] 400.6446AIC는 낮을수록 좋은 모델을 의미하며, 서로 다른 모델을 비교할 때 유용하다.
40.8 치매 데이터를 사용한 로지스틱 회귀 예제
치매 발생 여부를 나이에 따라 예측하는 로지스틱 회귀 모델을 만들어 보자. 이 예제에서는 치매 발생 여부(dementia)와 나이(age) 간의 관계를 분석한다.
이 데이터는 한국의 치매 유병률을 바탕으로 만든 가상 데이터이다.
library(readr)
dementia_age <- read_csv("./data/dementia.csv")
dementia_age$dementia <- as.factor(dementia_age$dementia)
dementia_age# A tibble: 100 × 3
id age dementia
<dbl> <dbl> <fct>
1 1 73 0
2 2 95 1
3 3 80 0
4 4 78 0
5 5 68 0
6 6 67 0
7 7 65 0
8 8 87 1
9 9 80 0
10 10 84 0
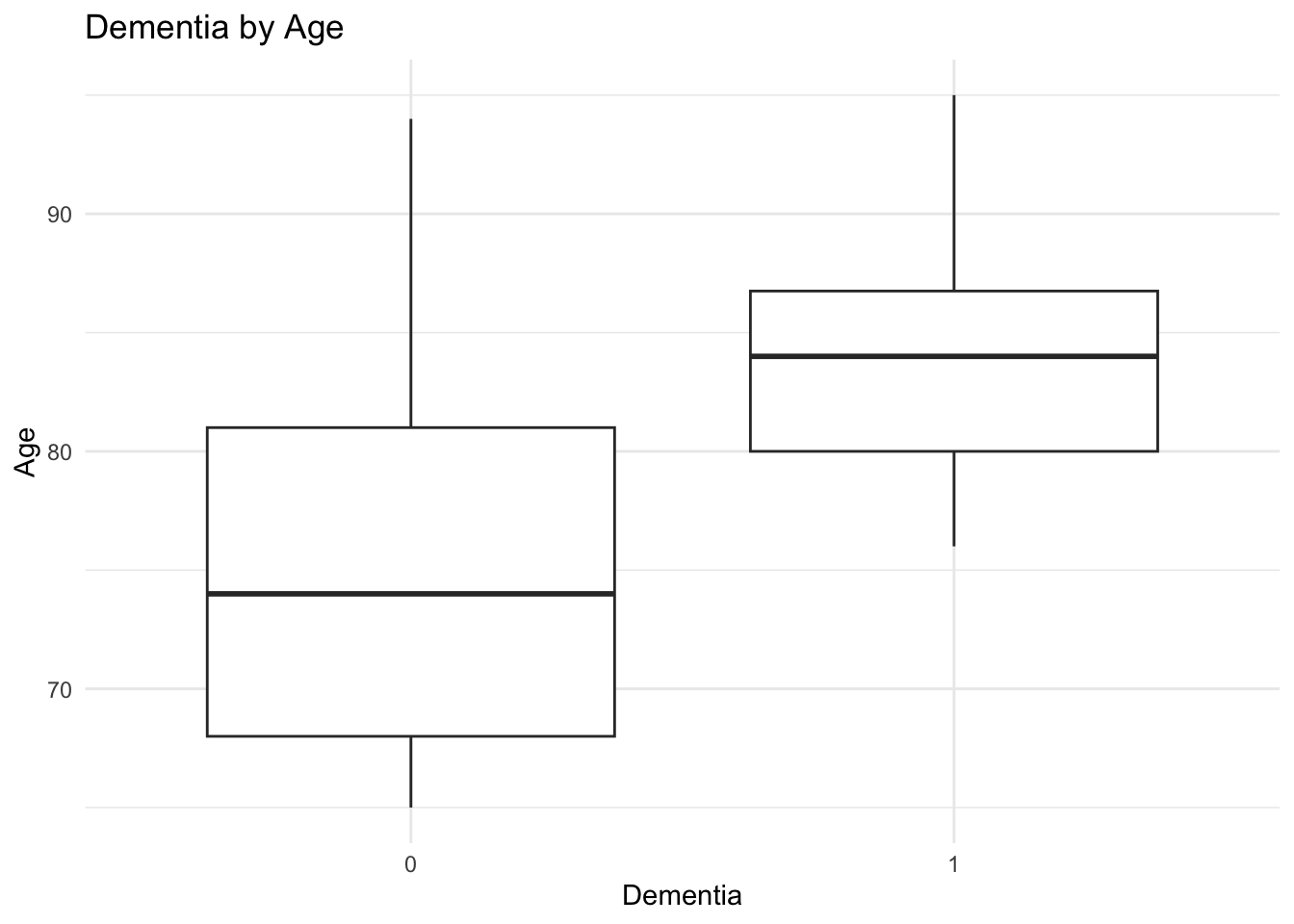
# ℹ 90 more rows이 데이터를 사용하여 연령과 치매 발생 여부 간의 관계를 시각화해 보자. 먼저 나이에 따른 치매 발생 여부를 박스 플롯으로 나타내 보자.
library(ggplot2)
ggplot(dementia_age, aes(x = dementia, y = age)) +
geom_boxplot() +
labs(title = "Dementia by Age", x = "Dementia", y = "Age") +
theme_minimal()로지스틱 회귀 모델을 실행해 보자. dementia를 결과 변수로 하고, age를 설명 변수로 설정한다.
Call:
glm(formula = dementia ~ age, family = binomial, data = dementia_age)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -14.44815 3.83290 -3.77 0.000164 ***
age 0.15858 0.04636 3.42 0.000625 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 80.993 on 99 degrees of freedom
Residual deviance: 65.158 on 98 degrees of freedom
AIC: 69.158
Number of Fisher Scoring iterations: 6결과를 보면 age의 계수는 약 0.15858이고, 절편(intercept)은 약 -14.44815이다. 이 모델은 나이가 증가함에 따라 치매 발생 확률이 증가한다는 것이 통계적으로 유의함을 알 수 있다.
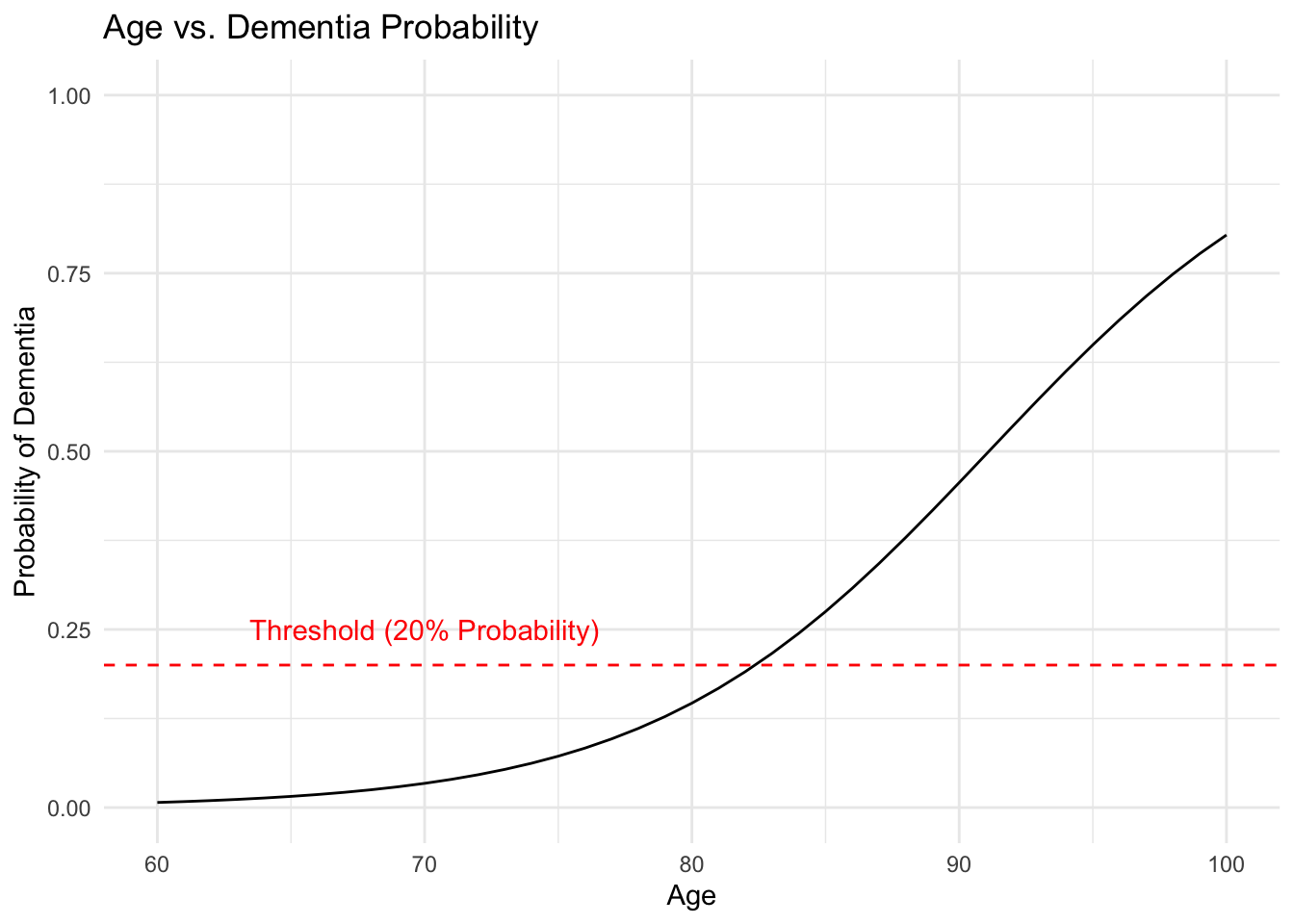
추정된 계수를 사용하여 나이에 따른 치매 발생 확률을 그래프로 보자.
# 나이에 따른 치매 발생 확률 계산
age_seq <- seq(60, 100, by = 1)
log_odds <- dementia_glm$coefficients[1] + dementia_glm$coefficients[2] * age_seq
probability <- 1 / (1 + exp(-log_odds))
data <- data.frame(age = age_seq, probability = probability)
ggplot(data, aes(x = age, y = probability)) +
geom_line() + labs(title = "Age vs. Dementia Probability", x = "Age", y = "Probability of Dementia") +
theme_minimal() +
ylim(0, 1) +
geom_hline(yintercept = 0.2, linetype = "dashed", color = "red") +
annotate("text", x = 70, y = 0.25, label = "Threshold (20% Probability)", color = "red")40.8.1 Risk(확률)과 Relative Risk
위 그래프를 수식으로 표현하면 다음과 같다.
\[ p = \frac{1}{1 + e^{-(-14.44815 + 0.15858 \cdot \text{age})}} \]
65세의 경우 치매 발생 확률을 계산해 보자.
age <- 65
log_odds <- dementia_glm$coefficients[1] + dementia_glm$coefficients[2] * age
probability_65 <- as.numeric(1 / (1 + exp(-log_odds)))
probability_65[1] 0.0156650970세의 경우 치매 발생 확률을 계산해 보자.
age <- 70
log_odds <- dementia_glm$coefficients[1] + dementia_glm$coefficients[2] * age
probability_70 <- as.numeric(1 / (1 + exp(-log_odds)))
probability_70[1] 0.033972675세의 경우 치매 발생 확률을 계산해 보자.
age <- 75
log_odds <- dementia_glm$coefficients[1] + dementia_glm$coefficients[2] * age
probability_75 <- as.numeric(1 / (1 + exp(-log_odds)))
probability_75[1] 0.072108480세의 경우 치매 발생 확률을 계산해 보자.
age <- 80
log_odds <- dementia_glm$coefficients[1] + dementia_glm$coefficients[2] * age
probability_80 <- as.numeric(1 / (1 + exp(-log_odds)))
probability_80[1] 0.146558770세가 65세보다 치매 발생 확률이 높다는 것을 확인할 수 있는데, 얼마나 높은지 Relative Risk(Risk Ratio)를 계산해 보자.
# Relative Risk (Risk Ratio) 계산
relative_risk <- probability_70 / probability_65
relative_risk[1] 2.16868275세와 70세의 Relative Risk를 계산해 보자.
# Relative Risk (Risk Ratio) 계산
relative_risk_75_70 <- probability_75 / probability_70
relative_risk_75_70[1] 2.12254675세와 80세의 Relative Risk를 계산해 보자.
# Relative Risk (Risk Ratio) 계산
relative_risk_80_75 <- probability_80 / probability_75
relative_risk_80_75[1] 2.03247740.8.2 Odds와 Odds Ratio
65세의 odds를 계산해 보자.
# Odds 계산
odds_65 <- probability_65 / (1 - probability_65)
odds_65[1] 0.0159143970세의 odds를 계산해 보자.
# Odds 계산
odds_70 <- probability_70 / (1 - probability_70)
odds_70[1] 0.0351673275세의 odds를 계산해 보자.
# Odds 계산
odds_75 <- probability_75 / (1 - probability_75)
odds_75[1] 0.0777120965세와 70세의 Odds Ratio를 계산해 보자.
# Odds Ratio 계산
odds_ratio_70_65 <- odds_70 / odds_65
odds_ratio_70_65[1] 2.20978175세와 70세의 Odds Ratio를 계산해 보자.
# Odds Ratio 계산
odds_ratio_75_70 <- odds_75 / odds_70
odds_ratio_75_70[1] 2.209781Odds Ratio(OR)와 Relative Risk(RR)는 모두 두 그룹 간의 위험을 비교하는 데 사용된다. 로지스틱 회귀 모델을 사용하는 경우에 Relative Risk는 구간에 따라 따른 값을 보이는 반면, Odds Ratio는 항상 일정한 값을 보인다.
40.9 Jamovi로 로지스틱 회귀 실행
Jamovi는 R을 기반으로 한 오픈 소스 통계 소프트웨어로, 로지스틱 회귀 분석을 쉽게 수행할 수 있는 인터페이스를 제공한다. Jamovi에서 로지스틱 회귀를 실행하는 방법은 다음과 같다.
40.9.1 데이터 불러오기
Jamovi를 실행하고 Open 버튼을 클릭하여 dementia.csv 파일을 불러온다. 이 파일은 치매 발생 여부와 나이 정보를 포함한다. 이 데이터는 깃허브 사이트1에서 다운로드할 수 있다.
참고로 Jamovi는 다양한 데이터 형식을 지원하며, CSV 파일을 쉽게 불러올 수 있다. 엑셀 파일, SPSS 파일, SAS 파일 등도 지원한다.
CSV 파일은 데이터를 쉼표로 구분하여 저장하는 텍스트 파일 형식이다. 각 행은 데이터의 한 레코드를 나타내며, 각 열은 변수(필드)를 나타낸다. CSV 파일은 간단하고 널리 사용되는 데이터 형식으로, 다양한 소프트웨어에서 쉽게 읽고 쓸 수 있다. 엑셀로 쉽게 열 수 있고, 엑셀 데이터도 CSV 형식으로 저장할 수 있다.
CSV 파일은 다음과 같은 형식을 가진다.
이름,나이,성별
홍길동,30,남
김영희,25,여
이순신,40,남각 행은 쉼표로 구분된 값들로 구성되어 있으며, 첫 번째 행은 변수의 이름을 나타낸다. Jamovi에서는 CSV 파일을 불러올 때 자동으로 변수의 이름을 인식하고, 데이터를 표 형식으로 표시한다.
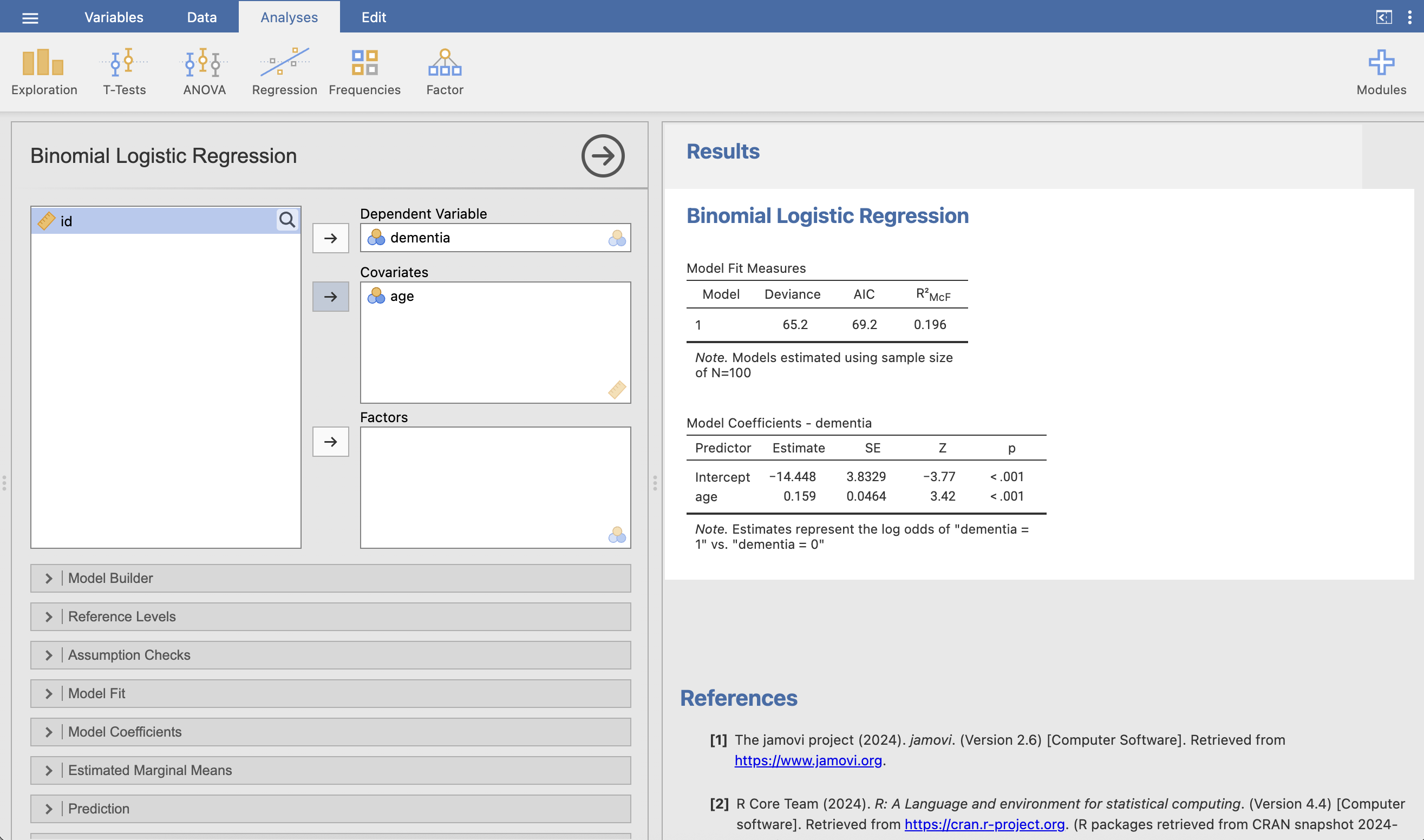
40.9.2 로지스틱 회귀 분석 실행
데이터를 불러온 후 Analyses 탭을 클릭하고, Regression 메뉴에서 Logistic Regression을 선택한다. 왼쪽 패널에서 dementia 변수를 Dependent Variable로, age 변수를 Covariates로 설정한다. 그러면 자동으로 로지스틱 회귀 모델이 생성되어 오른쪽 패널에서 결과를 확인할 수 있다.